コラム・特集
「三角比の計算」をおさらいしよう 〜古代エジプトの叡智から最新GNSS測量まで〜【測量のことイチから解説】

測量の歴史は「三角比」との深い結びつきから始まり、その関係は現代に至るまで続いている。
古代文明の驚異的建造物から最新のGNSS技術まで、三角比は測量の根幹を支え続けてきた。
そして今なお、測量士・測量士補試験において重要な出題項目となっている。
本記事では、この不朽の数学的概念「三角比」に焦点を当て、測量における重要性を改めて探る。
基礎的な原理から実践的な応用まで、測量に携わるプロフェッショナルが押さえるべき「三角比」の知識を体系的に解説する。
さらに、時代とともに進化してきた測量手法の変遷を辿りながら、三角比が果たしてきた役割と、今後の展望についても考察する。
ひとくちに「測量」と言っても、その手法は歴史とともに変化してきた。
三角測量や三辺測量といった種類があるが、これらはいずれも三角形の性質を利用している。
測量の原点と言われる、古代エジプトでピラミッドの高さを測った際にも三角形の性質を利用していた。
その性質とは、一つは二等辺になる直角三角形、もう一つは相似だ。
ピラミッドの高さを測った数学者タレスは、まっすぐに立てた棒とその影の長さが同じになる時間帯があることに気づいた。
そしてこの原理を利用すれば、ピラミッドの高さを測れるのではないかと考えたのだ。
 (画像:Canva)
(画像:Canva)
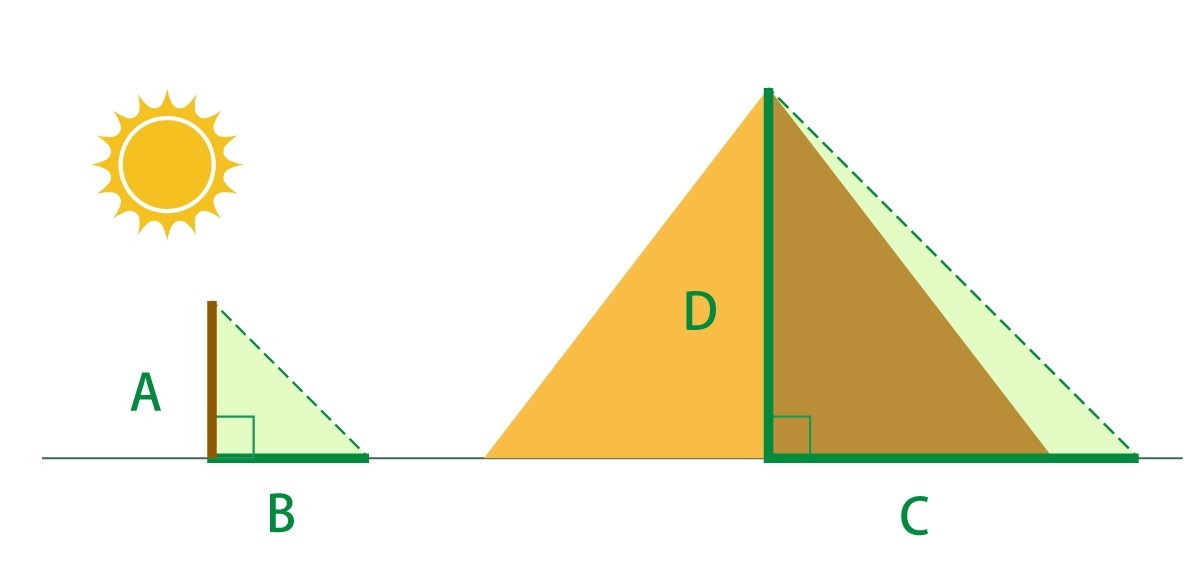
まっすぐに立てた棒Aと等しい長さの影Bが作った三角形は、「直角二等辺三角形」である。
そして、これと陽の差す角度が同じタイミングでピラミッドの影の長さCを測ればピラミッドの高さDを調べられるという推論は「相似」を利用している。
タレスの編み出した測量方法はその後、一つの辺とその両端の角の角度から直接測れない点までの距離を計算する「三角測量」へと発展し、長らく世界中で使用されてきた。
その後、1950年代に入り、レーザーを用いて距離を測定する装置「光波測距儀」が開発され、測距の精度が格段に向上。
国内で1974年から始められた第三次基本測量長期計画では、三角測量に代わり、「三辺測量」方式が採用された。
光波測距儀はその後、いわゆるトータルステーション(TS)として普及していく。
「三辺測量」はその名の通り、三角形の辺の長さを基準にした測量手法である。
ただし、実際の測量作業では測点に座標を付与するために角度も測る。
三角比でまず押さえておきたい知識は「相似」である。
相似の条件は2つあり、一つは「3つの辺の比がすべて等しいこと」である。
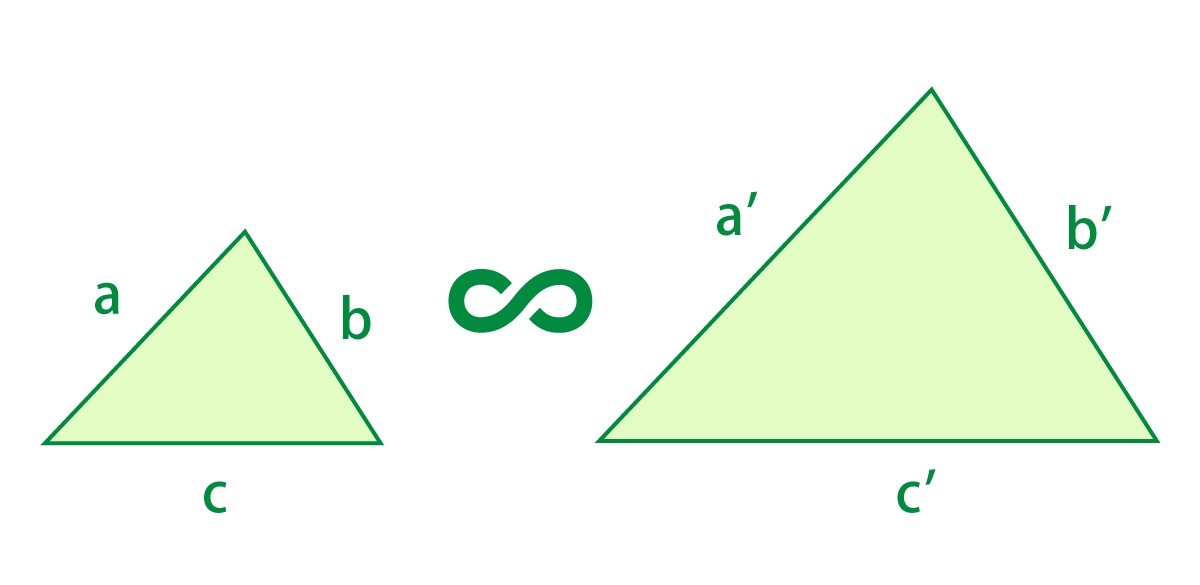
もう一つは、「2組の辺の比とその間の角がそれぞれ等しい」ことである。
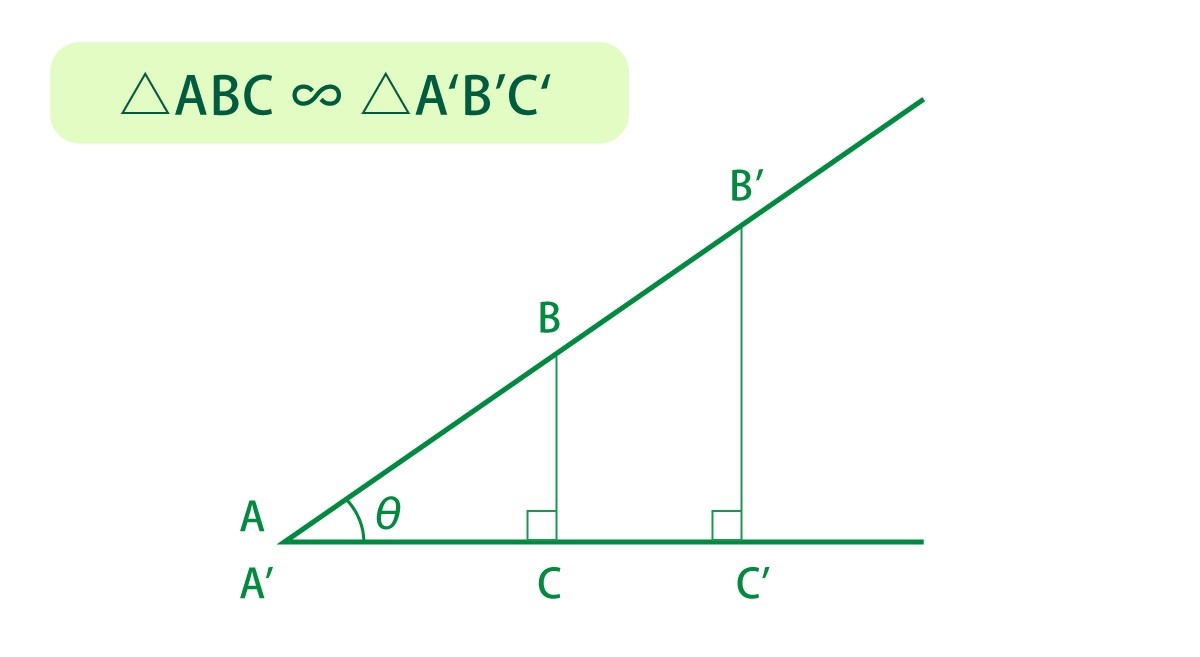
「三角比」で押さえておきたい知識がもうひとつある。「直角三角形」は「角度が決まると、比が決まる」という性質だ。
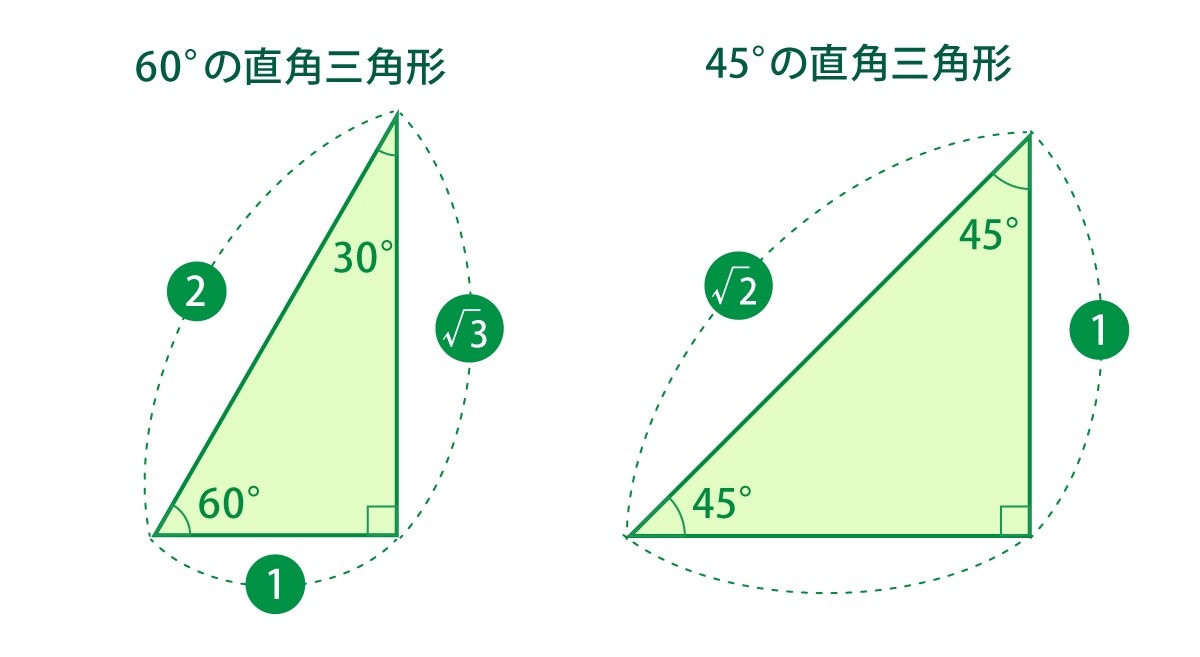
三角定規でもおなじみの、この2種類の直角三角形の辺の比はぜひとも覚えておきたい。
続いては、三角比の実用編として、三角比を使った面積や高さの求め方を紹介しよう。
三辺測量は三角比の「ヘロンの公式」を活用して面積を求めている。
3辺の長さがa、b、cの三角形の面積(T)を求めるとき、
T = √s (s-a) (s-b) (s-c)
ただし s= (a+b+c)÷2
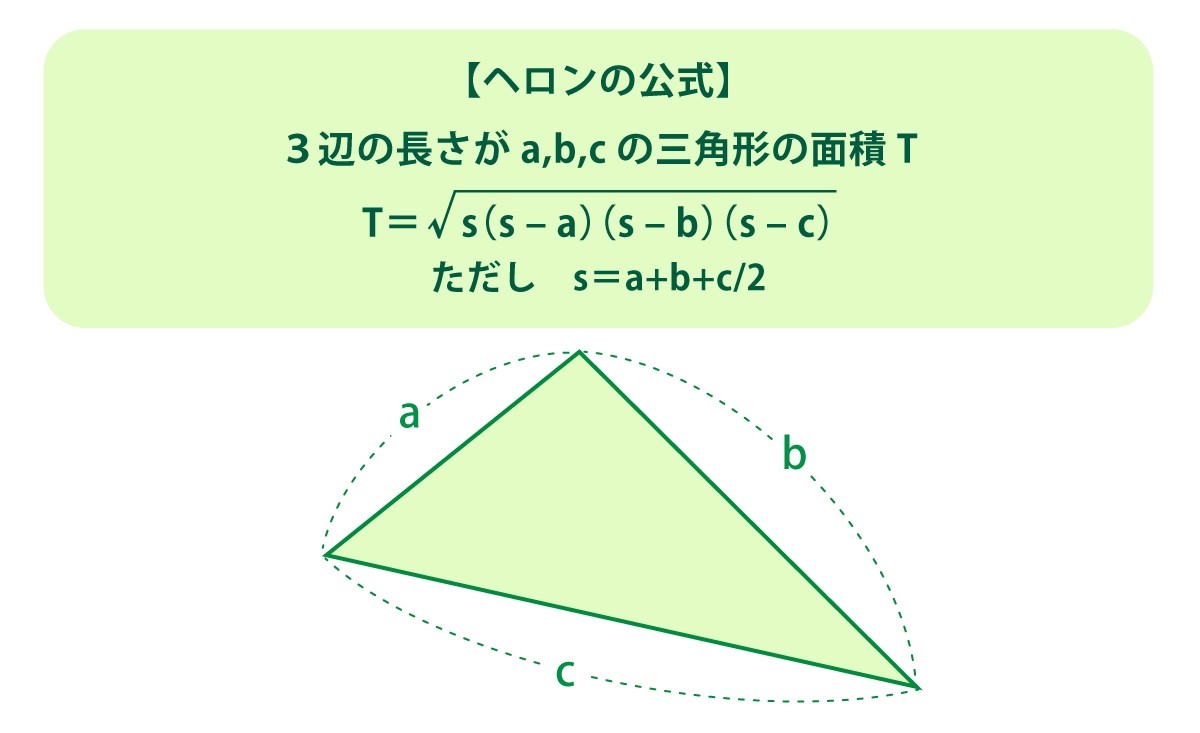
例えば、上の三角形の辺a、b、cがそれぞれ、a=3、b=4、c=5だった場合、面積Tはいくつになるか?
※まずは「ただし」部分の計算を行い、ルート式内のsに当てはまる数を求める。
s=(3+4+5)÷2=6
※次に面積Tを求める公式に数を当てはめて計算する。
T=√6(6-3)(6-4)(6-5)=√6×3×2×1=√36=6
この三角形の面積は6㎡(平方メートル)となる。
物の高さを測る場合は、原始的な手法ではピラミッドの高さを測ったタレスの手法に習い、45度の二等辺三角形ができる地点の距離を測る手法がある。
近代的な道具を使うなら、トータルステーション(TS)で「斜距離」「鉛直角」「水平角」を測り、これらの数値と三角比の公式を用いることで水平距離や高低差を求めることもできる。
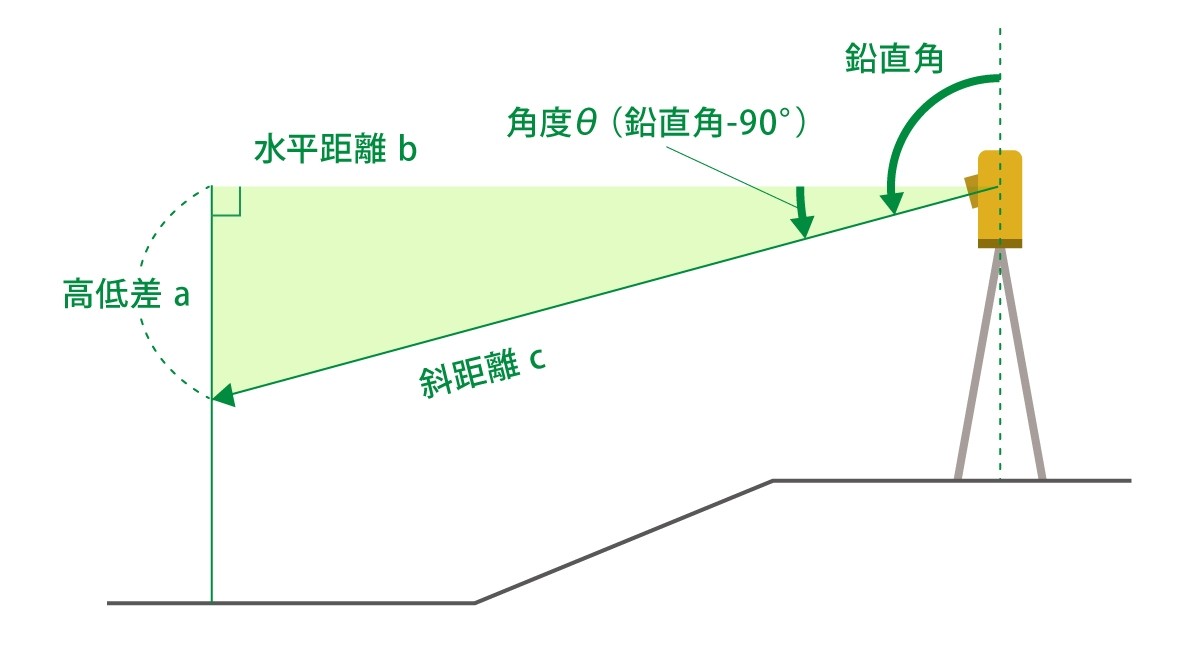
水平距離は、直角と角度Θの間の辺の長さで、斜辺cの長さがわかっているのでコサインの定義(cosΘ=水平距離/斜距離)を使うとよい。
高低差を求める場合は、サインの定義(sinΘ=高低差/斜辺)もしくは水平距離を算出したうえでタンジェントの定義(tanΘ=高低差/水平距離)で求めることができる。
測量に関する知識で、三角比で押さえるべきポイントがもう一つある。「比例式」だ。
比例式を使う計算は、測量士補試験でも出題されている。たとえば、上記の三角形から三角形の高さxを求める。
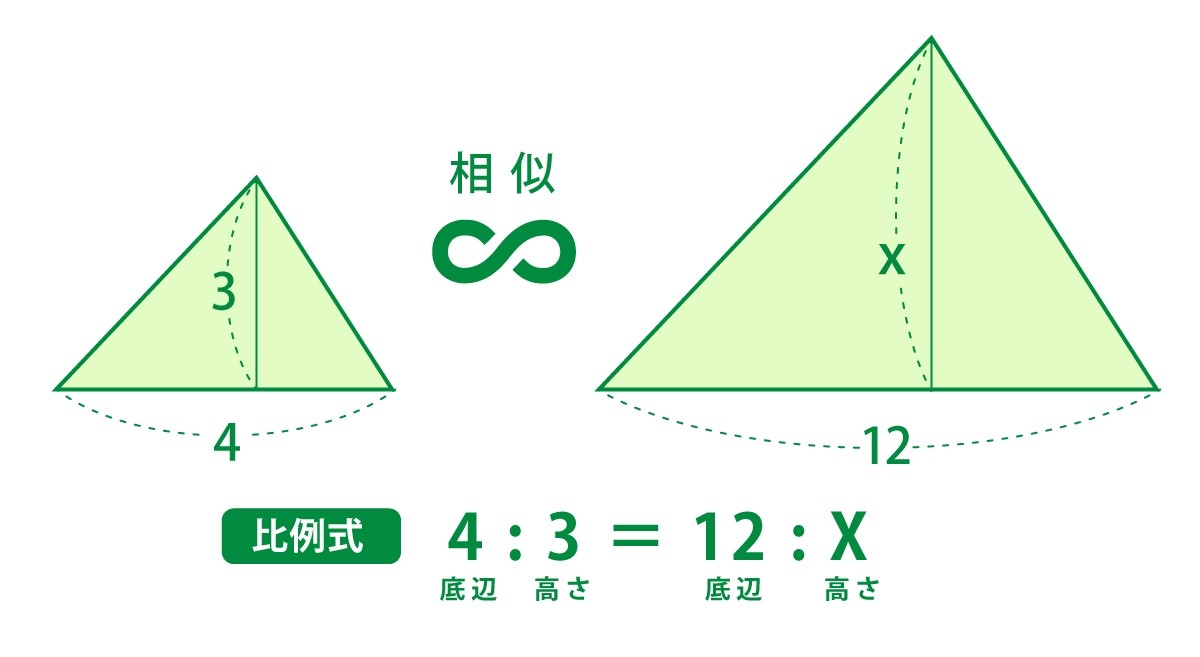
小さい三角形の底辺:高さ=大きい三角形の底辺:高さ
比例式は、外側と外側の数を掛けたものと、内側と内側の数を掛けたものが等しくなる。
4×x=3×12
4x=36
x=9
高さxは9となる。
上記のような高さを求める場合以外に、辺の長さがわかっている三角形Aと相似のA´では、
三角形Aの底辺:斜辺=三角形A´の底辺:斜辺
底辺A×斜辺A´=斜辺A×底辺A´
のような式でxを求めることができる。
前項までに三角形の性質や三角比の計算を紹介してきた。
測量士(補)の試験でも三角比を使う計算問題が出されるが、過去問題を繰り返し解いて解法に慣れていくのが王道といえる。
一方で、実務の面でいえば近年はGNSS測量が普及し、三角比の知識を使わなくても測量ができてしまう手法は増えてきている。
スマホ測量アプリ「OPTiM Geo Scan」は測量作業に必要な機材は、スマホやタブレット※1とGNSSレシーバーだけだ。
※1…iPhone proシリーズのスマートフォンもしくはiPad proシリーズのタブレットが対象。

測量作業の進め方も、従来のトータルステーションを用いるケースとはかなり様子が異なる。
スマホやタブレットを手に持ち、測量したい範囲を動画撮影するように画面に映す。
5〜6m間隔でGNSSレシーバを地面に置き「標定点」を設定。それを写真撮影するように画面上でタップする。

たった一人で、測量範囲をぐるっと歩き回るだけで測量はあっという間に終了だ。
トータルステーションのように、基準点合わせや水平の調整といった手間はなく、ターゲットを支える補助員も必要ない。
「OPTiM Geo Scan」は、スマホやタブレットで動画撮影したり、ゲームアプリを楽しんだりしたことがある人なら容易に操作できるようなユーザビリティが特徴だ。
測量したデータは、現地ですぐにチェックできるのはもちろん、クラウドにアップすることでほぼリアルタイムで遠隔地からでもデータを確認することができる。

3次元データだけでなく、座標データを取得したいという場合には、無料オプション機能「OPTiM Geo Point」を使うといい。
これは杭打ちにも便利で、現場にて目標地点まで誘導してくれる機能を備えている。
また、同じく無料オプション機能である「OPTiM Geo Desgin」は、Geo ScanやGeo Pointで取得した測量データを元に図化ができる機能だ。平面・縦横断図を作成できる。
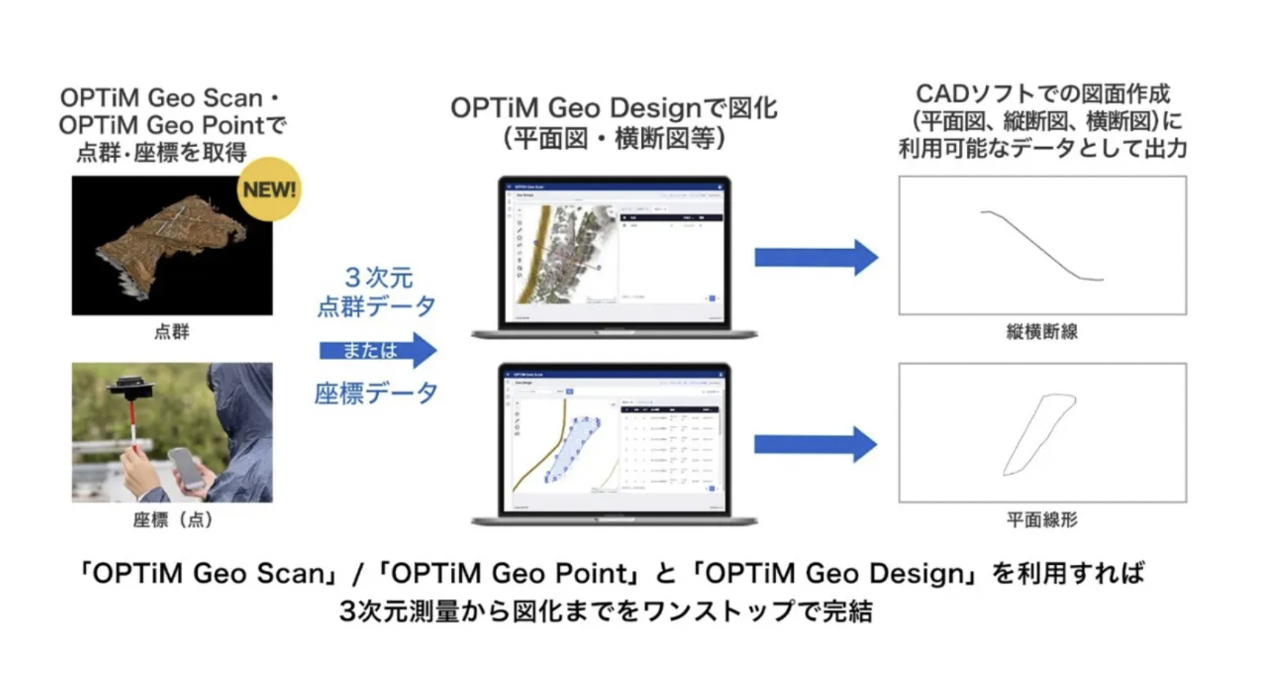
「OPTiM Geo Scan」は国土交通省の出来形管理要領に準拠しているので実用性が高い。
ハンディサイズでありながら高精度の測量データを計測でき、効率的に図化作成までできる機能が揃っている。
スマホ測量アプリ「OPTiM Geo Scan」を試すことで、従来の測量手法からの進化を感じてみてはいかがだろうか。
古代文明の驚異的建造物から最新のGNSS技術まで、三角比は測量の根幹を支え続けてきた。
そして今なお、測量士・測量士補試験において重要な出題項目となっている。
本記事では、この不朽の数学的概念「三角比」に焦点を当て、測量における重要性を改めて探る。
基礎的な原理から実践的な応用まで、測量に携わるプロフェッショナルが押さえるべき「三角比」の知識を体系的に解説する。
さらに、時代とともに進化してきた測量手法の変遷を辿りながら、三角比が果たしてきた役割と、今後の展望についても考察する。
測量と三角形の関係
ひとくちに「測量」と言っても、その手法は歴史とともに変化してきた。
三角測量や三辺測量といった種類があるが、これらはいずれも三角形の性質を利用している。
測量の原点と言われる、古代エジプトでピラミッドの高さを測った際にも三角形の性質を利用していた。
その性質とは、一つは二等辺になる直角三角形、もう一つは相似だ。
ピラミッドの高さを測った数学者タレスは、まっすぐに立てた棒とその影の長さが同じになる時間帯があることに気づいた。
そしてこの原理を利用すれば、ピラミッドの高さを測れるのではないかと考えたのだ。
 (画像:Canva)
(画像:Canva)まっすぐに立てた棒Aと等しい長さの影Bが作った三角形は、「直角二等辺三角形」である。
そして、これと陽の差す角度が同じタイミングでピラミッドの影の長さCを測ればピラミッドの高さDを調べられるという推論は「相似」を利用している。

タレスの編み出した測量方法はその後、一つの辺とその両端の角の角度から直接測れない点までの距離を計算する「三角測量」へと発展し、長らく世界中で使用されてきた。
その後、1950年代に入り、レーザーを用いて距離を測定する装置「光波測距儀」が開発され、測距の精度が格段に向上。
国内で1974年から始められた第三次基本測量長期計画では、三角測量に代わり、「三辺測量」方式が採用された。
光波測距儀はその後、いわゆるトータルステーション(TS)として普及していく。
「三辺測量」はその名の通り、三角形の辺の長さを基準にした測量手法である。
ただし、実際の測量作業では測点に座標を付与するために角度も測る。
三角比の“基礎の基礎”-「相似」と「直角三角形」
三角比でまず押さえておきたい知識は「相似」である。
相似とは?
ある図形を拡大もしくは縮小したとき、辺が同じ比率で変化し、角の角度はどれも変わらない。元の図形と拡大・縮小した図形が合同になる関係のこと
ある図形を拡大もしくは縮小したとき、辺が同じ比率で変化し、角の角度はどれも変わらない。元の図形と拡大・縮小した図形が合同になる関係のこと
相似の条件は2つあり、一つは「3つの辺の比がすべて等しいこと」である。

もう一つは、「2組の辺の比とその間の角がそれぞれ等しい」ことである。

「三角比」で押さえておきたい知識がもうひとつある。「直角三角形」は「角度が決まると、比が決まる」という性質だ。

- 45度の直角三角形は、辺の比が「1:1:√2」
- 60度の直角三角形は、辺の比が「1:2:√3」
三角定規でもおなじみの、この2種類の直角三角形の辺の比はぜひとも覚えておきたい。
三角比を使って「面積」「高さ」を測量する
続いては、三角比の実用編として、三角比を使った面積や高さの求め方を紹介しよう。
三角比を使った面積の調べ方
三辺測量は三角比の「ヘロンの公式」を活用して面積を求めている。
ヘロンの公式とは?
3つの辺の長さから面積を求める計算式である。
3つの辺の長さから面積を求める計算式である。
3辺の長さがa、b、cの三角形の面積(T)を求めるとき、
T = √s (s-a) (s-b) (s-c)
ただし s= (a+b+c)÷2

例えば、上の三角形の辺a、b、cがそれぞれ、a=3、b=4、c=5だった場合、面積Tはいくつになるか?
※まずは「ただし」部分の計算を行い、ルート式内のsに当てはまる数を求める。
s=(3+4+5)÷2=6
※次に面積Tを求める公式に数を当てはめて計算する。
T=√6(6-3)(6-4)(6-5)=√6×3×2×1=√36=6
この三角形の面積は6㎡(平方メートル)となる。
三角比を使った高さの調べ方
物の高さを測る場合は、原始的な手法ではピラミッドの高さを測ったタレスの手法に習い、45度の二等辺三角形ができる地点の距離を測る手法がある。
近代的な道具を使うなら、トータルステーション(TS)で「斜距離」「鉛直角」「水平角」を測り、これらの数値と三角比の公式を用いることで水平距離や高低差を求めることもできる。

水平距離は、直角と角度Θの間の辺の長さで、斜辺cの長さがわかっているのでコサインの定義(cosΘ=水平距離/斜距離)を使うとよい。
高低差を求める場合は、サインの定義(sinΘ=高低差/斜辺)もしくは水平距離を算出したうえでタンジェントの定義(tanΘ=高低差/水平距離)で求めることができる。
測量士補試験に出る「比例式」の求め方をおさらい
測量に関する知識で、三角比で押さえるべきポイントがもう一つある。「比例式」だ。
比例式とは?
相似の関係にある2つの三角形の辺の長さや高さを求める計算式
相似の関係にある2つの三角形の辺の長さや高さを求める計算式
比例式を使う計算は、測量士補試験でも出題されている。たとえば、上記の三角形から三角形の高さxを求める。

小さい三角形の底辺:高さ=大きい三角形の底辺:高さ
比例式は、外側と外側の数を掛けたものと、内側と内側の数を掛けたものが等しくなる。
4×x=3×12
4x=36
x=9
高さxは9となる。
上記のような高さを求める場合以外に、辺の長さがわかっている三角形Aと相似のA´では、
三角形Aの底辺:斜辺=三角形A´の底辺:斜辺
底辺A×斜辺A´=斜辺A×底辺A´
のような式でxを求めることができる。
三角比がわからなくても高精度な測量ができるスマホ測量アプリ「OPTiM Geo Scan」
前項までに三角形の性質や三角比の計算を紹介してきた。
測量士(補)の試験でも三角比を使う計算問題が出されるが、過去問題を繰り返し解いて解法に慣れていくのが王道といえる。
一方で、実務の面でいえば近年はGNSS測量が普及し、三角比の知識を使わなくても測量ができてしまう手法は増えてきている。
スマホ測量アプリ「OPTiM Geo Scan」は測量作業に必要な機材は、スマホやタブレット※1とGNSSレシーバーだけだ。
※1…iPhone proシリーズのスマートフォンもしくはiPad proシリーズのタブレットが対象。

測量作業の進め方も、従来のトータルステーションを用いるケースとはかなり様子が異なる。
スマホやタブレットを手に持ち、測量したい範囲を動画撮影するように画面に映す。
5〜6m間隔でGNSSレシーバを地面に置き「標定点」を設定。それを写真撮影するように画面上でタップする。

たった一人で、測量範囲をぐるっと歩き回るだけで測量はあっという間に終了だ。
トータルステーションのように、基準点合わせや水平の調整といった手間はなく、ターゲットを支える補助員も必要ない。
測量作業だけじゃない!データ確認や図化作成もスマホで楽々!
「OPTiM Geo Scan」は、スマホやタブレットで動画撮影したり、ゲームアプリを楽しんだりしたことがある人なら容易に操作できるようなユーザビリティが特徴だ。
測量したデータは、現地ですぐにチェックできるのはもちろん、クラウドにアップすることでほぼリアルタイムで遠隔地からでもデータを確認することができる。

3次元データだけでなく、座標データを取得したいという場合には、無料オプション機能「OPTiM Geo Point」を使うといい。
これは杭打ちにも便利で、現場にて目標地点まで誘導してくれる機能を備えている。
また、同じく無料オプション機能である「OPTiM Geo Desgin」は、Geo ScanやGeo Pointで取得した測量データを元に図化ができる機能だ。平面・縦横断図を作成できる。

「OPTiM Geo Scan」は国土交通省の出来形管理要領に準拠しているので実用性が高い。
ハンディサイズでありながら高精度の測量データを計測でき、効率的に図化作成までできる機能が揃っている。
スマホ測量アプリ「OPTiM Geo Scan」を試すことで、従来の測量手法からの進化を感じてみてはいかがだろうか。
参考:
https://www.jsurvey.jp/soknohi/sok-nenpyou.htm
https://www.gsi.go.jp/common/000076686.pdf https://www.try-it.jp/chapters-1294/sections-1295/ https://www.su-gaku.net/enjoy/library_mathsearch02/
https://www.jsurvey.jp/soknohi/sok-nenpyou.htm
https://www.gsi.go.jp/common/000076686.pdf https://www.try-it.jp/chapters-1294/sections-1295/ https://www.su-gaku.net/enjoy/library_mathsearch02/
WRITTEN by

三浦 るり
2006年よりライターのキャリアをスタートし、2012年よりフリーに。人材業界でさまざまな業界・分野に触れてきた経験を活かし、幅広くライティングを手掛ける。現在は特に建築や不動産、さらにはDX分野を探究中。
大人気シリーズ!【いまさら聞けない?】測量のことイチから解説 〜 連載記事一覧 〜
- 「三角比の計算」をおさらいしよう 〜古代エジプトの叡智から最新GNSS測量まで〜【測量のことイチから解説】
建設土木のICT活用など、
デジコンからの最新情報をメールでお届けします







































