コラム・特集
測量における【交会法】とは?前方 / 側方 / 後方交会法の違いと使い分けも紹介!【測量のことイチから解説】
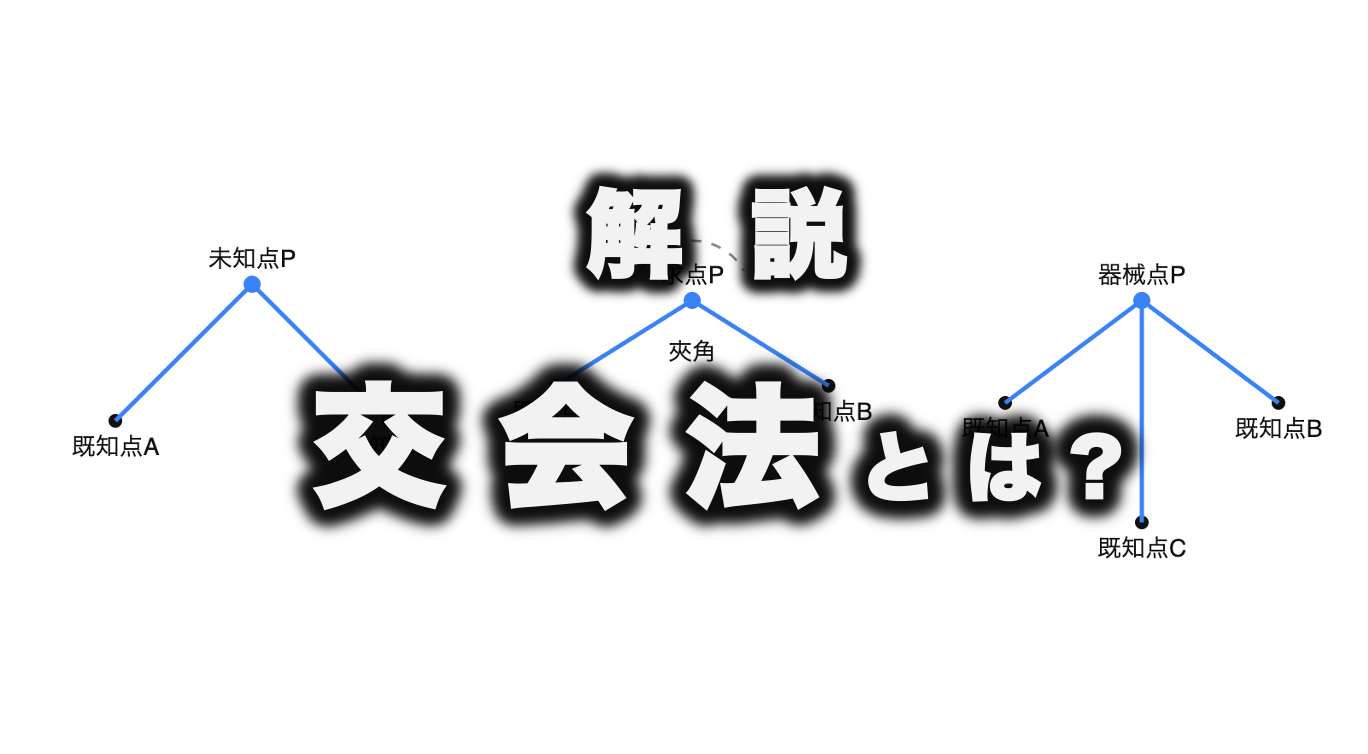

交会法(こうかいほう)とは、2点または3点以上の既知点から未知点への測線を引き、交点の位置を求める測量方法の総称である。
距離測定を行わず、主に方向を視準すること(角度を測ること)によって目標点の位置を決定する。
簡単に言えば、「位置がわかっている複数の目印を使って、未知の場所の正確な位置を計算で求める」という測量技術だ。
交会法は平板測量で最もよく用いられてきた方法であり、現代ではトータルステーション(TS)などの電子測量機器を使って、より高精度な測量が可能になっている。
交会法は、測量機器をどこに設置するかによって、前方交会法、側方交会法、後方交会法の3種類に分類される。
それぞれ異なる特徴と用途を持ち、測量の目的や現場の状況に応じて使い分けられる。
2点以上の既知点に測量機器を置いて、未知点(目標)を視準し、視準方向が交わる点を目標の位置として定める方法である。
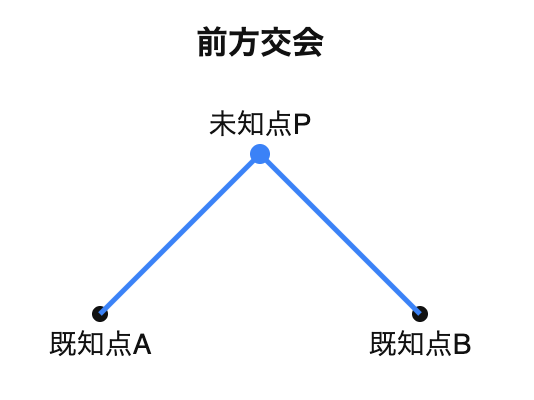
イメージとしては、2つの見晴らし台(既知点)から、遠くにある目標物の方向を測定し、その2つの方向線が交わる点として目標物の位置を特定する方法だ。
求点から2個の既知点の夾角(きょうかく:2つの線が作る角度)と、その1つから未知点への方向線を定めて求点の位置を求める測量法である。
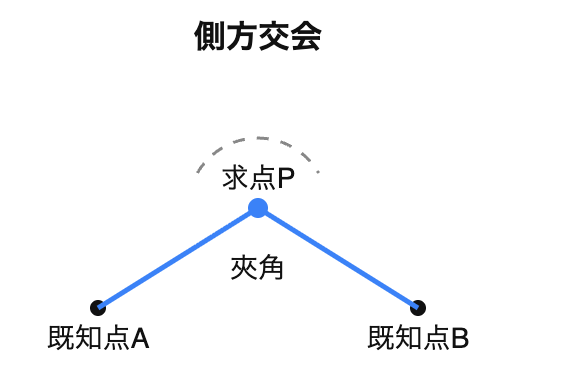
後方交会法と前方交会法を組み合わせたような方法といえる。
未知点(器械点)に測量機器を据えて、複数の既知点を視準し、器械点の位置を定める方法である。本記事では、この後方交会法を中心に詳しく解説する。
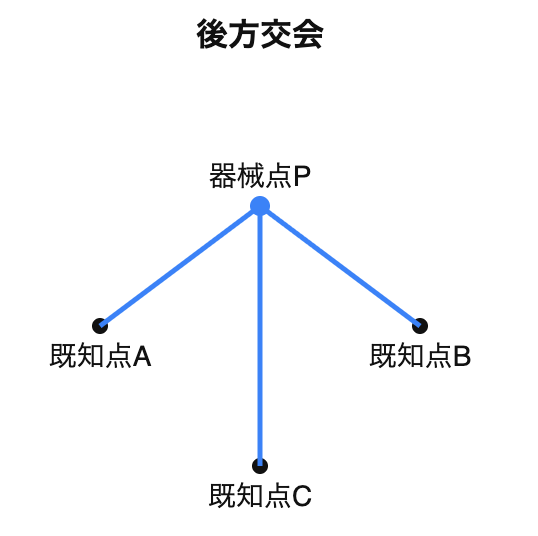
簡単に言えば、「自分がいる場所の座標を知りたいときに、周りに見える既知の目印を測って、自分の位置を逆算する」という方法だ。
航海中の船が山の重なり具合から自分の位置を特定する「山立て」という古い手法が、この原理の原型となっている。
本記事では、交会法の中でも特に実務での使用頻度が高い後方交会法について、以降のセクションで詳しく解説する。
後方交会法が現場で重宝される理由は、以下の通りである。
後方交会法の詳細解説 —— 測量手順から計算原理まで
ここからは、後方交会法に焦点を当てて、実務に必要な知識を詳しく解説していく。
後方交会法では、原理的には2点の既知点でも計算可能だが、幾何学的な安定性と検証性の観点から3点以上の既知点を使用することが推奨される。このため「三点法」とも呼ばれる。
既知点の数を増やすほど、観測の冗長度(データの重複性)が増し、最小二乗法による精度向上が期待できる。実務では3〜4点を使用することが多い。
後方交会法による測量作業は、以下の手順で実施される。各ステップを丁寧に行うことが、精度の高い測量結果を得るための鍵となる。
後方交会法の計算原理を、高校数学の知識で理解できるように説明する。
後方交会法では、既知点と器械点を結ぶ三角形の幾何学的関係を利用する。
使用する数学的手法には、正弦定理、余弦定理、三平方の定理、三角関数などがある。
例えば、2点の既知点A、Bがあり、器械点Pからそれぞれの点までの距離と、2点の間の角度(夾角)を測定した場合、三角形ABPの形状が完全に決まる。
既知点A、Bの座標がわかっているので、この三角形の幾何関係から器械点Pの座標を逆算できる。
3点以上の既知点を使用する場合、複数の三角形から器械点の座標が計算される。
しかし、観測誤差により、各三角形から得られる座標値は完全には一致しない。
そこで最小二乗法という統計的手法を用いる。これは、すべての観測データを総合的に評価し、誤差の二乗和が最小になるような「最も確からしい」座標値を求める方法である。
最小二乗法を用いると、以下のメリットがある。
後方交会法には、幾何学上の重要な制約が存在する。それが「危険円」と呼ばれる現象である。
既知点と器械点(求点)が同一の円周上に並ぶ場合、解が不定になるという制約がある。
これは円の性質から来る幾何学的な制約で、円周上のどの点から見ても、円に内接する弦が作る角度(円周角)は一定になるためである。
わかりやすく言えば、既知点3点が描く三角形に対して、器械点の位置がある特定の円周上にあると、角度の測定結果だけでは器械点の位置を一意に決定できなくなるのだ。
同一円周上の問題を避けるため、以下の対策を講じる。
測量の品質を確保するため、実務では具体的な基準が設けられている。
出来形管理用のトータルステーションにおける後方交会の運用では、既知点間の狭角を30°〜150°に制限する扱いが示された事例がある。
これは、幾何学的安定性を確保するための実務上の目安である。
角度が30°より狭い(狭角)、または150°より広い(広角)場合、わずかな観測誤差が座標計算結果に大きな影響を与えやすくなる。
品質の高い後方交会測量を実施するため、以下の点を確認する。
測量精度を向上させるため、以下の冗長化を図る。
公共測量を実施する場合、国土地理院が定める「作業規程の準則」に準拠する必要がある。
後方交会法に関しても、本体規程および付録(現場試験基準、計算式集、標準様式)に従って実施・記録する。
地上型レーザースキャナ等の標定方式の一つとしても、作業規程の準則に後方交会法が位置づけられている。
実務では、さまざまなエラーが発生する可能性がある。代表的なエラーとその対策を理解しておくことが重要である。
トータルステーションは、角度を測る電子セオドライトと距離を測る光波距離計を組み合わせた測量機器である。
1台で角度(鉛直角・水平角)と距離を同時に測定でき、後方交会法による器械設置機能を標準搭載した機種が多い。
近年のトータルステーションは内部にコンピュータを搭載し、後方交会法の計算を自動的に実行し、器械点座標と標準偏差を即座に表示する。
トータルステーションから発射されたレーザー光を反射させるための測量用具。既知点の位置に設置し、距離測定の精度を高める。ピンポールプリズムや一素子プリズムなどの種類がある。
トータルステーションを安定して設置するための器具。測量中の振動や傾きを防ぎ、器械を水平に保つ。
後方交会法のメリットとデメリット
これまで解説してきた交会法は、測量の基本となる重要な測量法である。
しかし、既知点の選定、幾何配置の検討、観測、計算といった一連の作業には、専門的な知識と経験が必要とされてきた。
近年、こうした従来の測量手法を大きく変革する技術として、GNSS(Global Navigation Satellite System)測量を活用したスマホ測量アプリが登場している。
その代表例がスマホ測量アプリ「OPTiM Geo Scan」である。

GNSS測量とは、GPSをはじめとする複数の衛星測位システムからの信号を受信し、位置情報を三角測量の原理で計算する方法である。
従来の交会法とは異なり、地上の既知点を設置・視準する必要がなく、衛星信号が受信できる場所であれば、短時間で位置情報を取得できる。
これにより、交会法で必要だった以下の作業が不要になる。
OPTiM Geo Scanは、LiDAR(Light Detection And Ranging:光による検知・測距)センサー搭載のiPhoneと、GNSSレシーバーを組み合わせることで、簡単・短時間で高精度な測量を実現する画期的なサービスである。
 (GNSSレシーバー)
(GNSSレシーバー)

OPTiM Geo Scanのような新技術は、測量業務を大きく変革する可能性を秘めているが、すべての測量現場で従来手法を置き換えられるわけではない。
以下のように、状況に応じた使い分けが重要である。
従来の交会法を含む測量技術は、高度な専門知識と豊富な経験が必要とされ、属人性の高い業務であった。

ベテラン技術者の減少と若手技術者の不足が課題となる中、OPTiM Geo Scanのような技術は、測量業務の標準化と効率化を推進する重要な役割を果たしている。
交会法は、既知点を利用して未知点の位置を求める基本的な測量技術である。前方交会法、側方交会法、後方交会法の3種類があり、それぞれ測量の目的に応じて使い分けられる。
中でも後方交会法は、任意の位置に測量機器を設置できる自由度の高さから、現代の測量現場で最も頻繁に使用される方法である。
既設の基準点を活用しながら、測量対象を見渡せる最適な位置から効率的に作業できる点が大きな強みである。
ただし、幾何学的な制約(同一円周上の問題)や、角度配置による精度の変動など、注意すべき点も多い。測量の目的や求められる精度に応じて、適切な既知点の選定、観測の冗長化、品質管理を行うことが重要である。
高精度が求められる構造物測量などでは、既知点上への器械設置など、より確実な方法を選択することが推奨される。一方、土工事などの現場測量や、測量対象を広く見渡せる位置からの測量には、後方交会法が非常に有効である。
公共測量を実施する際は、国土地理院が定める「作業規程の準則」などの基準に従い、適切な測量方法と機器を選択し、記録を正確に残すことが求められる。
距離測定を行わず、主に方向を視準すること(角度を測ること)によって目標点の位置を決定する。
簡単に言えば、「位置がわかっている複数の目印を使って、未知の場所の正確な位置を計算で求める」という測量技術だ。
交会法は平板測量で最もよく用いられてきた方法であり、現代ではトータルステーション(TS)などの電子測量機器を使って、より高精度な測量が可能になっている。
交会法は、測量機器をどこに設置するかによって、前方交会法、側方交会法、後方交会法の3種類に分類される。
それぞれ異なる特徴と用途を持ち、測量の目的や現場の状況に応じて使い分けられる。
交会法の3つの種類と特徴は?
前方交会法(Forward Intersection)
2点以上の既知点に測量機器を置いて、未知点(目標)を視準し、視準方向が交わる点を目標の位置として定める方法である。

イメージとしては、2つの見晴らし台(既知点)から、遠くにある目標物の方向を測定し、その2つの方向線が交わる点として目標物の位置を特定する方法だ。
《 前方交会法の主な用途 》
《 前方交会法の特徴 》
- 地形図作成における地形点(細部点)の決定
- 河川や谷など、直接アクセスが困難な場所の測量
- 複数の未知点を既知点側から効率的に求める場合
《 前方交会法の特徴 》
- 既知点側に測量機器を設置するため、安定した基準点上で作業できる
- 遠方の未知点を複数測定する際に効率的
- 測量機器を未知点に移動させる必要がない
側方交会法(Side Intersection)
求点から2個の既知点の夾角(きょうかく:2つの線が作る角度)と、その1つから未知点への方向線を定めて求点の位置を求める測量法である。

後方交会法と前方交会法を組み合わせたような方法といえる。
《 側方交会法の主な用途 》
《 側方交会法の特徴 》
- 前方交会と後方交会の両方の要素が必要な特殊な測量
- 既知点の配置が限定的な場合の補助的手法
《 側方交会法の特徴 》
- 前方交会法と後方交会法の中間的な性質を持つ
- 実務での使用頻度は他の2つに比べて少ない
後方交会法(Resection)
未知点(器械点)に測量機器を据えて、複数の既知点を視準し、器械点の位置を定める方法である。本記事では、この後方交会法を中心に詳しく解説する。

簡単に言えば、「自分がいる場所の座標を知りたいときに、周りに見える既知の目印を測って、自分の位置を逆算する」という方法だ。
航海中の船が山の重なり具合から自分の位置を特定する「山立て」という古い手法が、この原理の原型となっている。
《 後方交会法の主な用途 》
《後方交会法の 特徴 》
- 測量対象を見渡せる任意の位置からの測量
- 既設基準点を活用した迅速な位置確立
- 地上レーザースキャナなどの標定(位置決定)
- トラバース測量で多角点がない場合の補助手段
《後方交会法の 特徴 》
- 測量したい対象が最もよく見える場所に機器を設置できる
- 既知点上に機器を設置する必要がないため、作業の自由度が高い
- 現場で最も頻繁に使用される交会法
なぜ後方交会法が現場でよく使われるのか?
本記事では、交会法の中でも特に実務での使用頻度が高い後方交会法について、以降のセクションで詳しく解説する。
後方交会法が現場で重宝される理由は、以下の通りである。
- 任意位置への設置の自由度:測量対象が最も見やすい場所を選んで機器を据えられる
- 既設基準点の有効活用:周囲にある街区基準点や工事基準点を、そこに機器を置かずに活用できる
- GNSS不利環境での有効性:樹木の下や高層ビル街など、衛星測位が難しい場所でも使える
- 作業効率の向上:機器の移動回数を減らせるため時間短縮につながる
後方交会法の詳細解説 —— 測量手順から計算原理まで
ここからは、後方交会法に焦点を当てて、実務に必要な知識を詳しく解説していく。必要観測と既知点数
後方交会法では、原理的には2点の既知点でも計算可能だが、幾何学的な安定性と検証性の観点から3点以上の既知点を使用することが推奨される。このため「三点法」とも呼ばれる。
既知点の数を増やすほど、観測の冗長度(データの重複性)が増し、最小二乗法による精度向上が期待できる。実務では3〜4点を使用することが多い。
後方交会法の測量手順
後方交会法による測量作業は、以下の手順で実施される。各ステップを丁寧に行うことが、精度の高い測量結果を得るための鍵となる。
1. 既知点の選定
まず、測量に使用する既知点を選定する。原則として3点以上を採用し、以下の条件を満たす点を選ぶ。
まず、測量に使用する既知点を選定する。原則として3点以上を採用し、以下の条件を満たす点を選ぶ。
- 視通が確保できる:器械点から各既知点が明瞭に見えること
- 角度バランスが良い:既知点同士が極端な狭角や広角にならないこと
- 距離バランスが良い:既知点までの距離が極端に偏らないこと
2. 器械の据付
選定した未知点(これから座標を求める器械点)にトータルステーションなどの測量機器を設置する。この際、以下の作業を正確に行う。
選定した未知点(これから座標を求める器械点)にトータルステーションなどの測量機器を設置する。この際、以下の作業を正確に行う。
- 求心:器械の中心を測点の真上に合わせる
- 整準:器械を水平に保つ
- 器械高の記録:地面から器械の中心までの高さを正確に測定・記録する
3. 観測
各既知点に対して、方向角(水平角)を観測する。必要に応じて距離も測定する。
各既知点に対して、方向角(水平角)を観測する。必要に応じて距離も測定する。
- 最初の既知点を視準した際に水平角度を0°にセットする
- 次の既知点を視準し、夾角(2点間の角度)を記録する
- 各既知点までの距離も測定する(角度のみでも計算可能だが、距離も測定すると精度が向上する)
- 外れ値を抑制するため、反復観測を行うことが推奨される
4. 計算
観測したデータをもとに、器械点の座標を計算する。
観測したデータをもとに、器械点の座標を計算する。
- 角観測のみの場合:既知点間の幾何関係と観測角から、図解法または解析法で未知点を解く。
- 角+距離の場合:角度と距離の混合観測方程式を立て、最小二乗法で器械点の座標(X座標、Y座標)を推定する。現代のトータルステーションでは、機器内部で最小二乗推定と標準偏差(σ)の表示を自動的に行う実装が一般的である。
5. 検定(品質確認)
計算結果の妥当性を検証する。
異常値が検出された場合は、観測の除外、既知点の追加、または再計算を実施する。
計算結果の妥当性を検証する。
- 残差の確認:観測値と計算値の差が許容範囲内か確認する
- 標準偏差の確認:推定精度を示す指標が基準を満たしているか確認する
- 幾何チェック:角度差の比較など、幾何学的な整合性を確認する
異常値が検出された場合は、観測の除外、既知点の追加、または再計算を実施する。
後方交会法の計算原理をわかりやすく解説
後方交会法の計算原理を、高校数学の知識で理解できるように説明する。
基本的な幾何学
後方交会法では、既知点と器械点を結ぶ三角形の幾何学的関係を利用する。
使用する数学的手法には、正弦定理、余弦定理、三平方の定理、三角関数などがある。
例えば、2点の既知点A、Bがあり、器械点Pからそれぞれの点までの距離と、2点の間の角度(夾角)を測定した場合、三角形ABPの形状が完全に決まる。
既知点A、Bの座標がわかっているので、この三角形の幾何関係から器械点Pの座標を逆算できる。
最小二乗法による精度向上
3点以上の既知点を使用する場合、複数の三角形から器械点の座標が計算される。
しかし、観測誤差により、各三角形から得られる座標値は完全には一致しない。
そこで最小二乗法という統計的手法を用いる。これは、すべての観測データを総合的に評価し、誤差の二乗和が最小になるような「最も確からしい」座標値を求める方法である。
最小二乗法を用いると、以下のメリットがある。
- 観測の冗長度(データの重複性)が増し、精度が向上する
- 標準偏差など、推定精度を示す指標が得られる
- 外れ値(異常な観測データ)の影響を抑制できる
幾何学上の重要な制約——「危険円」とは
後方交会法には、幾何学上の重要な制約が存在する。それが「危険円」と呼ばれる現象である。
同一円周上の問題
既知点と器械点(求点)が同一の円周上に並ぶ場合、解が不定になるという制約がある。
これは円の性質から来る幾何学的な制約で、円周上のどの点から見ても、円に内接する弦が作る角度(円周角)は一定になるためである。
わかりやすく言えば、既知点3点が描く三角形に対して、器械点の位置がある特定の円周上にあると、角度の測定結果だけでは器械点の位置を一意に決定できなくなるのだ。
実務上の対策
同一円周上の問題を避けるため、以下の対策を講じる。
- 既知点の配置を確認し、器械点が危険円上に近づかないようにする
- 既知点と器械点が作る三角形が、できるだけ二等辺三角形に近い形になるよう器械を据える
- 既知点間の角度(器械点から見た夾角)が極端にならないようにする
角度条件と品質管理の実務ポイント
測量の品質を確保するため、実務では具体的な基準が設けられている。
既知点間の角度制限
出来形管理用のトータルステーションにおける後方交会の運用では、既知点間の狭角を30°〜150°に制限する扱いが示された事例がある。
これは、幾何学的安定性を確保するための実務上の目安である。
角度が30°より狭い(狭角)、または150°より広い(広角)場合、わずかな観測誤差が座標計算結果に大きな影響を与えやすくなる。
既知点配置の品質チェック
品質の高い後方交会測量を実施するため、以下の点を確認する。
- 三角形に対する配置:既知点が作る三角形に対して、器械点が極端に片寄らないこと
- 狭角・一直線配置の回避:既知点が一直線に近い配置や、極端な狭角配置を避ける
- 点数の確保:原則として3点以上、可能であれば4点以上の既知点を使用する
観測の冗長化
測量精度を向上させるため、以下の冗長化を図る。
- 既知点の追加:3点以上を使用し、多点化するほど冗長度が増す
- 反復観測:同じ既知点を複数回観測し、平均値を採用する
- 角度と距離の併用:角度だけでなく距離も測定することで、検証性が高まる
公共測量における準拠
公共測量を実施する場合、国土地理院が定める「作業規程の準則」に準拠する必要がある。
後方交会法に関しても、本体規程および付録(現場試験基準、計算式集、標準様式)に従って実施・記録する。
地上型レーザースキャナ等の標定方式の一つとしても、作業規程の準則に後方交会法が位置づけられている。
後方交会法で起こりやすいエラーと対策を紹介
実務では、さまざまなエラーが発生する可能性がある。代表的なエラーとその対策を理解しておくことが重要である。
既知点の角度配置が不適切
症状:
狭角、一直線配置、または同一円周上に近い配置により、計算結果の精度が著しく低下する、または解が不定になる。
対策:
狭角、一直線配置、または同一円周上に近い配置により、計算結果の精度が著しく低下する、または解が不定になる。
対策:
- 既知点の選定を見直し、角度バランスの良い点を選ぶ
- 既知点の数を増やし、冗長度を高める
- 器械点の位置を変更し、幾何配置を改善する
器械高・ミラー高の入力ミス
症状:
計算された座標の標高(Z座標)が異常な値になる。
対策:
計算された座標の標高(Z座標)が異常な値になる。
対策:
- 器械高とミラー高(反射鏡の高さ)を測定後、記録前に必ず再確認する
- 観測前後のダブルチェック体制を徹底する
- 標高の妥当性を、周辺の既知点と比較して確認する
方位設定の誤り
症状:
計算された平面座標(X、Y)が大きくずれる。
対策:
計算された平面座標(X、Y)が大きくずれる。
対策:
- 基準方向(北方向など)の取り違いに注意する
- 最初の既知点の方位を慎重に確認する
- 複数の既知点で方位を検証する
残差が大きい
症状:
観測値と計算値の差(残差)が許容範囲を超える。
対策:
観測値と計算値の差(残差)が許容範囲を超える。
対策:
- 外れ値(明らかに異常な観測データ)を除外する
- 既知点を追加し、観測データを増やす
- 最小二乗法で再計算し、整合性を回復する
- 必要に応じて再観測を実施する
交会法で使用する主な測量機器
トータルステーション(TS)
トータルステーションは、角度を測る電子セオドライトと距離を測る光波距離計を組み合わせた測量機器である。
1台で角度(鉛直角・水平角)と距離を同時に測定でき、後方交会法による器械設置機能を標準搭載した機種が多い。
近年のトータルステーションは内部にコンピュータを搭載し、後方交会法の計算を自動的に実行し、器械点座標と標準偏差を即座に表示する。
プリズム(反射鏡)
トータルステーションから発射されたレーザー光を反射させるための測量用具。既知点の位置に設置し、距離測定の精度を高める。ピンポールプリズムや一素子プリズムなどの種類がある。
三脚
トータルステーションを安定して設置するための器具。測量中の振動や傾きを防ぎ、器械を水平に保つ。
後方交会法のメリットとデメリット
《 メリット 》
《 デメリット 》
- 任意位置への設置:測量対象が最もよく見える場所を自由に選択できる
- 迅速な位置確立:既知点上に機器を設置する手間がなく、器械点を迅速に確定できる
- 作業効率の向上:機器の移動回数を減らせるため、作業時間が短縮される
- 柔軟な測量計画:障害物や地形条件に応じて、測量計画を柔軟に立てられる
《 デメリット 》
- 計算誤差の存在:観測データから間接的に座標を求めるため、計算上の誤差を含む
- 幾何配置への依存:既知点の配置や器械点の位置関係により、精度が大きく変動する
- 高精度測量には不向き:構造物測量など、ミリメートル単位の精度を要する作業には適さない場合がある
交会法が不要の新技術——スマホ測量アプリ「OPTiM Geo Scan」
これまで解説してきた交会法は、測量の基本となる重要な測量法である。
しかし、既知点の選定、幾何配置の検討、観測、計算といった一連の作業には、専門的な知識と経験が必要とされてきた。
近年、こうした従来の測量手法を大きく変革する技術として、GNSS(Global Navigation Satellite System)測量を活用したスマホ測量アプリが登場している。
その代表例がスマホ測量アプリ「OPTiM Geo Scan」である。

GNSS測量の基本原理
GNSS測量とは、GPSをはじめとする複数の衛星測位システムからの信号を受信し、位置情報を三角測量の原理で計算する方法である。
従来の交会法とは異なり、地上の既知点を設置・視準する必要がなく、衛星信号が受信できる場所であれば、短時間で位置情報を取得できる。
これにより、交会法で必要だった以下の作業が不要になる。
- 既知点の選定と配置の検討
- 幾何学的制約(危険円など)の考慮
- 角度・距離の視準観測
- 複雑な座標計算と検定作業
スマホ測量アプリ「OPTiM Geo Scan」の特徴
OPTiM Geo Scanは、LiDAR(Light Detection And Ranging:光による検知・測距)センサー搭載のiPhoneと、GNSSレシーバーを組み合わせることで、簡単・短時間で高精度な測量を実現する画期的なサービスである。
 (GNSSレシーバー)
(GNSSレシーバー)
1. 交会法が不要
従来の測量では、器械点の位置を確定するために後方交会法などの手法が必須だった。しかし、OPTiM Geo Scanでは、GNSS衛星からの信号により直接位置情報を取得するため、既知点を用いた交会法の手順が不要である。
2. 一人で完結するワンマン測量
アプリ「OPTiM Geo Point」を使用することで、iPhoneだけでGNSS測量と測量杭の設定が一人で完了する。従来の測量では複数人での作業が一般的だったが、人手不足が深刻化する建設業界において、大幅な省力化が実現できる。
3. 直感的な操作性
UI(ユーザー・インターフェイス)が非常にわかりやすく設計されており、ゲーム感覚で測量作業を行える。専門的な測量知識が少ない作業者でも、短時間で習熟できる点が大きな強みである。
4. 測量から図化まで一気通貫
図化機能「OPTiM Geo Design」と連携することで、測量から図面作成まで一気通貫で実施できる。データの受け渡しや変換の手間が省け、作業全体の効率が飛躍的に向上する。
5. 国土交通省の基準に準拠
精度面でも信頼性が高く、国土交通省の出来高管理要領に準拠している。公共工事での使用にも対応できる品質が確保されている。
従来の測量では、器械点の位置を確定するために後方交会法などの手法が必須だった。しかし、OPTiM Geo Scanでは、GNSS衛星からの信号により直接位置情報を取得するため、既知点を用いた交会法の手順が不要である。
2. 一人で完結するワンマン測量
アプリ「OPTiM Geo Point」を使用することで、iPhoneだけでGNSS測量と測量杭の設定が一人で完了する。従来の測量では複数人での作業が一般的だったが、人手不足が深刻化する建設業界において、大幅な省力化が実現できる。
3. 直感的な操作性
UI(ユーザー・インターフェイス)が非常にわかりやすく設計されており、ゲーム感覚で測量作業を行える。専門的な測量知識が少ない作業者でも、短時間で習熟できる点が大きな強みである。
4. 測量から図化まで一気通貫
図化機能「OPTiM Geo Design」と連携することで、測量から図面作成まで一気通貫で実施できる。データの受け渡しや変換の手間が省け、作業全体の効率が飛躍的に向上する。
5. 国土交通省の基準に準拠
精度面でも信頼性が高く、国土交通省の出来高管理要領に準拠している。公共工事での使用にも対応できる品質が確保されている。
従来の交会法との使い分け
OPTiM Geo Scanのような新技術は、測量業務を大きく変革する可能性を秘めているが、すべての測量現場で従来手法を置き換えられるわけではない。
以下のように、状況に応じた使い分けが重要である。
《 GNSS測量(OPTiM Geo Scanなど)が有利な場面 》
- 衛星信号を受信できる開けた場所
- 広範囲の測量を短時間で実施したい場合
- 測量要員が限られている現場
- 既知点の設置が困難な場所
《 従来の交会法(TS測量)が有利な場面 》
- 樹冠下や高層ビル街など、GNSS信号が受信しにくい環境
- ミリメートル単位の高精度が求められる構造物測量
- 既知点が十分に整備されている現場
- 狭い範囲での精密な測量
測量の属人性からの脱却
従来の交会法を含む測量技術は、高度な専門知識と豊富な経験が必要とされ、属人性の高い業務であった。

ベテラン技術者の減少と若手技術者の不足が課題となる中、OPTiM Geo Scanのような技術は、測量業務の標準化と効率化を推進する重要な役割を果たしている。
まとめ
交会法は、既知点を利用して未知点の位置を求める基本的な測量技術である。前方交会法、側方交会法、後方交会法の3種類があり、それぞれ測量の目的に応じて使い分けられる。
中でも後方交会法は、任意の位置に測量機器を設置できる自由度の高さから、現代の測量現場で最も頻繁に使用される方法である。
既設の基準点を活用しながら、測量対象を見渡せる最適な位置から効率的に作業できる点が大きな強みである。
ただし、幾何学的な制約(同一円周上の問題)や、角度配置による精度の変動など、注意すべき点も多い。測量の目的や求められる精度に応じて、適切な既知点の選定、観測の冗長化、品質管理を行うことが重要である。
高精度が求められる構造物測量などでは、既知点上への器械設置など、より確実な方法を選択することが推奨される。一方、土工事などの現場測量や、測量対象を広く見渡せる位置からの測量には、後方交会法が非常に有効である。
公共測量を実施する際は、国土地理院が定める「作業規程の準則」などの基準に従い、適切な測量方法と機器を選択し、記録を正確に残すことが求められる。
WRITTEN by

大人気シリーズ!【いまさら聞けない?】測量のことイチから解説 〜 連載記事一覧 〜
- 測量における【交会法】とは?前方 / 側方 / 後方交会法の違いと使い分けも紹介!【測量のことイチから解説】
