コラム・特集
等高線の基礎知識を押さえよう!〜点間距離の求め方など応用知識も紹介!〜【測量のことイチから解説】


シリーズ「測量のことイチから解説」。今回は、測量の中でも地形測量となじみ深い「等高線」について。
まずは「等高線とは?」というところから、地形図の読み方など基礎をおさらいしよう。
測量士補試験に出題される、等高線の点間距離求め方も解説を行う。記事の後半では、等高線や標高に関する最新技術についても紹介していく。
等高線(別名:コンターライン)とは、同じ高さの地点(標高)を結んだ線のことである。
間隔ごとに主曲線・計曲線・補助曲線の3種類の線があり、等高線からその場の地形を読み取ることができる。
主曲線・計曲線・補助曲線は線の太さや種類で見分けられるようになっている。
たとえば、5000分の1の地図では以下のような間隔で示される。
等高線の間隔が狭いと斜面は急で、広ければなだらかな地形である。
等高線は上空から地面を見下ろすかたちで、地形を表現するものだが、地形を横から見た「断面図」を作成することもできる。
等高線から地形が読み取れると前述したが、なんとなく地形の高低差の判別がつくだけではものたりない。
地形の最も高い部分の連なりを示す「尾根線」と、山と山の間の低地を結んだ「谷線」も覚えておこう。
まずは等高線の中から最も標高の高い位置(山頂)と、川の位置を確認しよう。
水は高いところから低いところへ流れることもあり、川は地図上で低地を示している。そして、川の流れる場所が谷線の位置とも言える。
とはいえ、もちろん川が流れていない谷地もある。谷線の見つけ方は、もう一つ、高地から低地へ向かってみたとき、等高線がくぼんだ形状の場所が谷である。
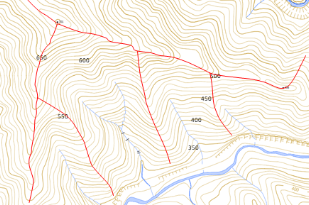 引用:国土交通省 国土地理院「地図を見て尾根と谷を読み解く」(https://www.gsi.go.jp/CHIRIKYOUIKU/one_tani.html)
引用:国土交通省 国土地理院「地図を見て尾根と谷を読み解く」(https://www.gsi.go.jp/CHIRIKYOUIKU/one_tani.html)
一方で、高地から低地に向かって見たときに、突き出した形状の地形の突端が尾根線である(上記図の赤線が尾根線)。
尾根線は山頂と山頂をつなぐ線でもあるので、図面上のもっとも高い位置(山頂)をまず見ると良い。
前項までに等高線に関する基礎知識を紹介してきた。
続いては、等高線に関する知識の活用法についてだ。
測量士補試験では、等高線の間隔(2点間の距離)を計算式で求める問題が出題されている。
よくある形式の例題を4つのステップに従い解いてみよう。
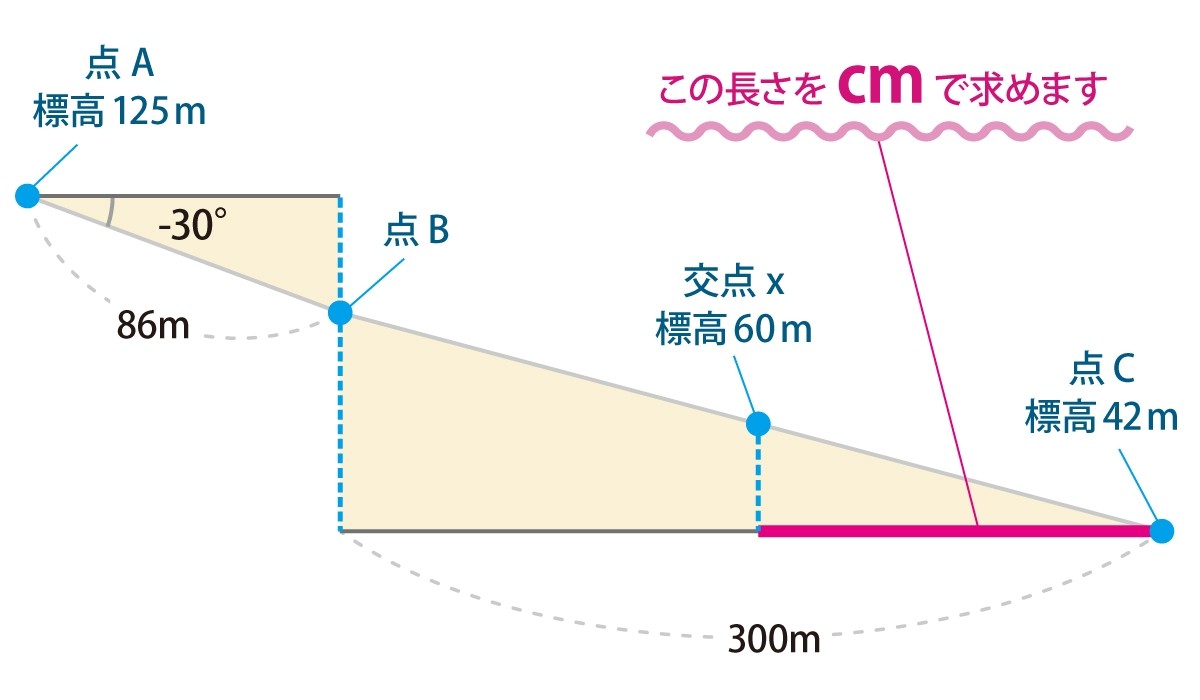
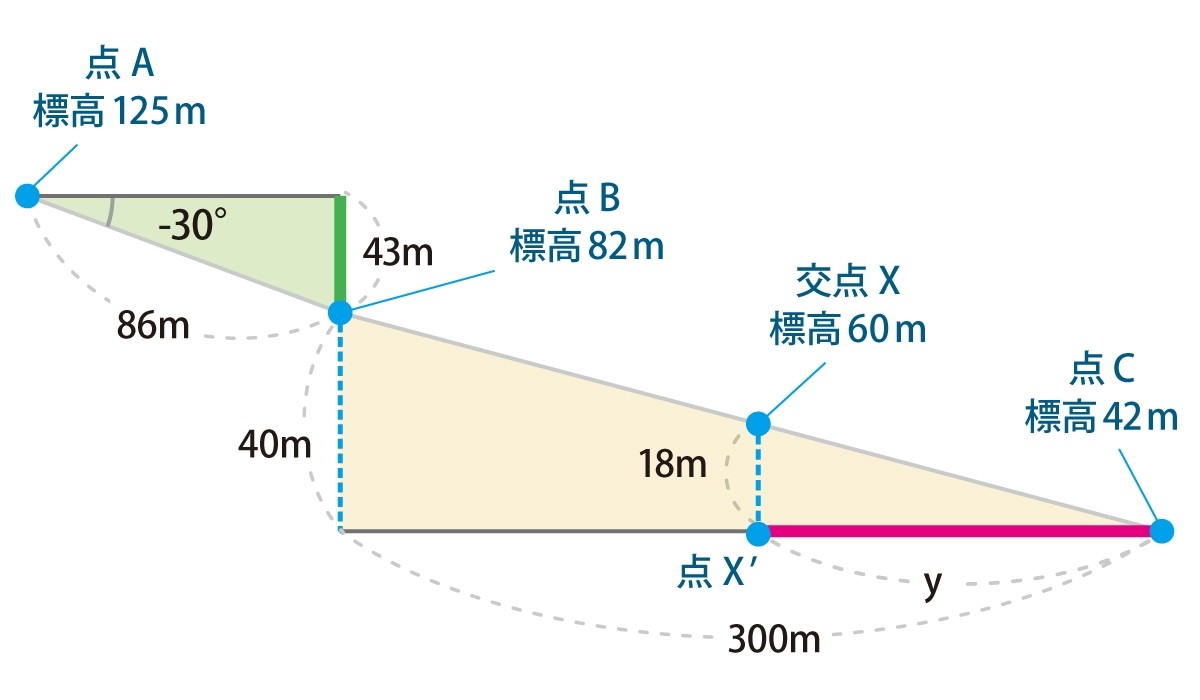
問題文を図で示すと上図になる。
問われているのは、交点xから垂直に降ろした点x´から点cまでの距離である。
一見難しく感じるかもしれないが、解法に慣れれば落ち着いて正解を出せるはずだ。
まずは、高低角-30°とAB間の斜距離86mを使って、標高125mから点Bまでの高低差(h)を求める。
三角比のsinΘの定義を使うと高低差hの部分(=対辺)を求められる。
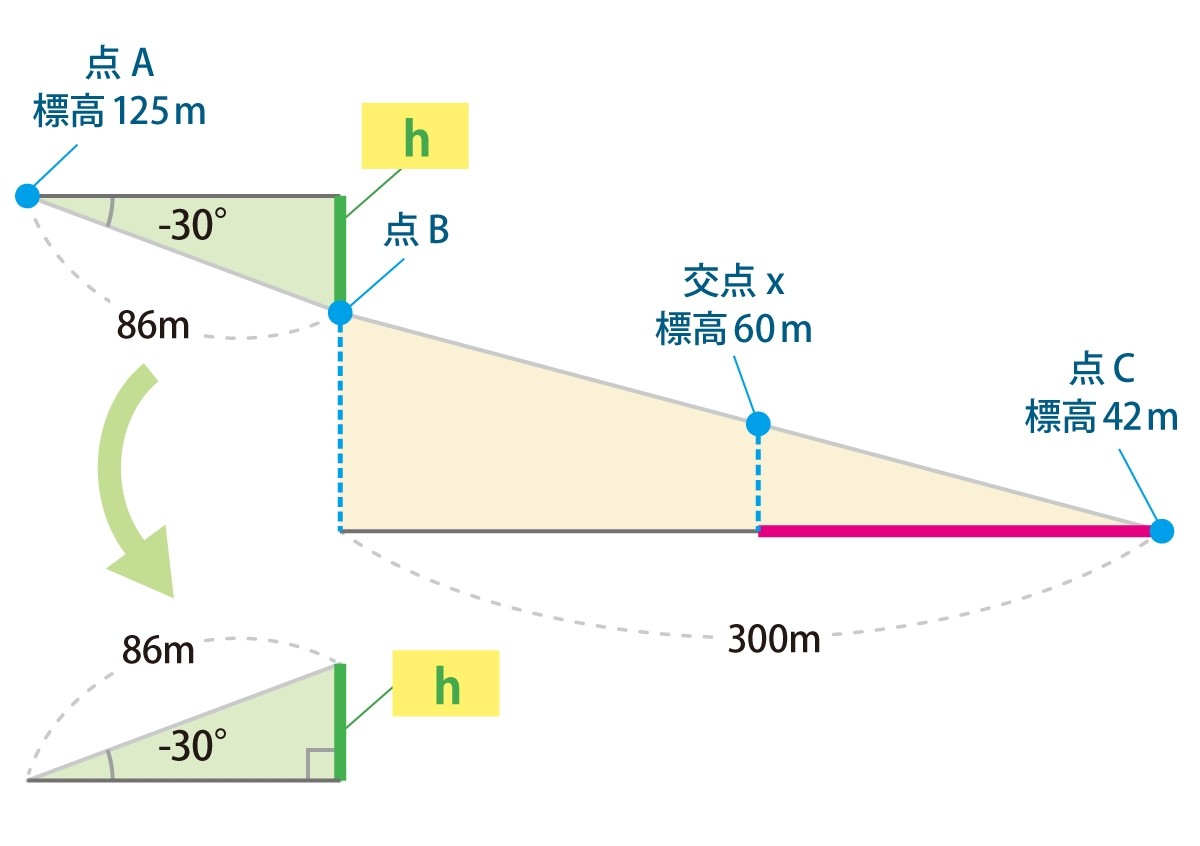
この三角形は30°の角をもつ直角三角形なので、sin30°の関数※「1/2(0.5)」を利用する。
※測量士(補)試験では、関数表が問題文に添えられているが、sin30°は代表的なので暗記するとよい。
ステップ1で標高125m地点と点Bまでの高低差を求めた。
続いては、点Bの標高を求める。
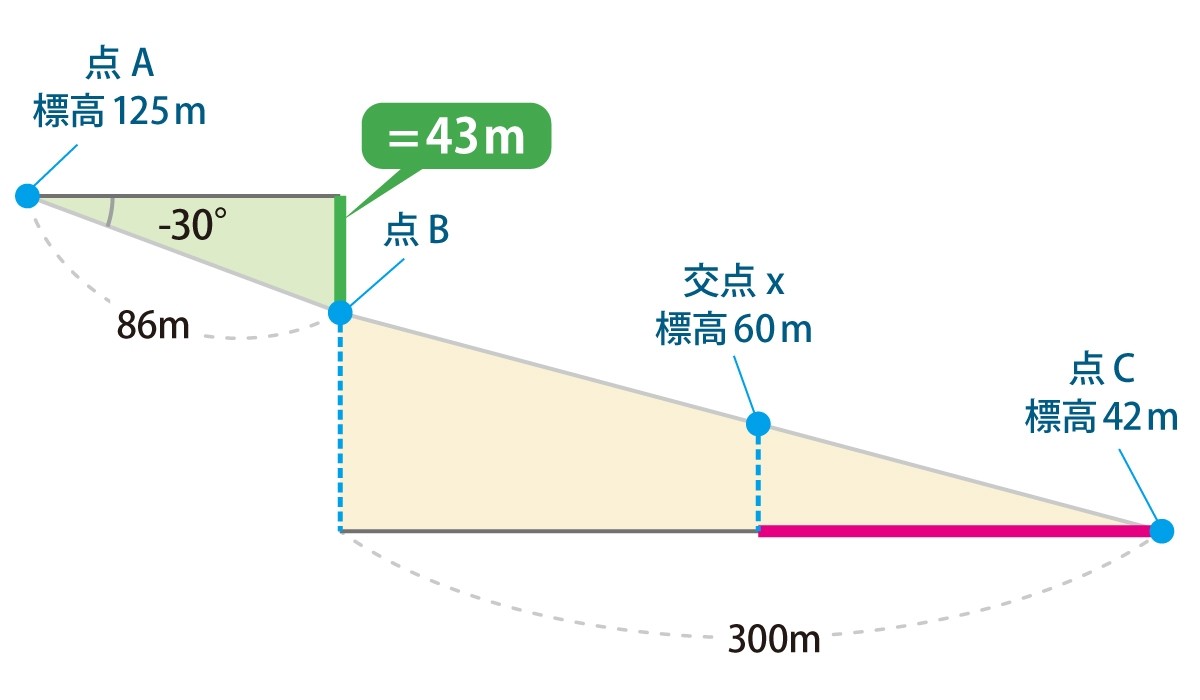
点Bを通る垂線を見れば、計算はシンプルだ。標高125mから43mを引けばよい。
点Bの標高は82mということがわかる。
次に、点Bから垂直に降ろされた線の長さを求める。こちらも引き算を使うだけだ。
点Bの標高82mから点cに示されている標高42mを引く。
大きい三角形の高低差は40mということがわかる。
ここから後半戦で、交点 x に関係する計算に突入する。
まずは、交点xから標高42mまでの高低差を出そう。
交点xは標高60mとわかっているので、引き算で求められる。
続いては三角比の比例式を使う。
点cと点bを斜辺に持つ大きな三角形と、点cと交点xを斜辺に持つ小さな三角形は角cが等しい相似の三角形である。
この2つの三角形の辺の長さを比例式にすることで、点x´から点cまでの長さ、つまり交点xと点cの水平距離を求める。
両辺の外側の数字同士、内側の数字同士を掛ける
交点xと点cの水平距離は135m
最後に、地形図の縮尺を条件に合わせて完成だ。
問題文に縮尺1/1000と書いてあるので、1000で割り、単位を㎝に揃える。
トータルステーション(TS)で慎重に観測し、標高や高低差を計算式で求めるというやり方は、伝統的な測量技術の一つ。
いまも測量士(補)国家資格を取るために習得すべき知識とされている。
しかし、実務においては、最新技術によって測量作業は効率化し、図面作成も素早くできるようになってきている。
3次元測量は、地上型レーザースキャナーやGNSS(人工衛星)を用いて3次元座標を取得し、それを活用して測量データを生成する。
複雑な地形に強く、1人で作業を完了させられるものも。また、取得したデータを様々な形で活用できるというメリットもある。
2022年には国土交通省が「3次元測量技術を用いた出来形管理要領(案)」の改訂版を策定し、“これからの測量技術”として注目が高まっている。

「OPTiM Geo Scan」は、iPhone pro/iPad proシリーズに搭載されているLiDARというレーザー計測技術を利用した3次元測量アプリで、スマホやタブレットとハンディサイズのGNSS受信器を使って1人で測量が行える。
手軽でありながら、出来形管理要領に準拠しており実用性は十分だ。
「OPTiM Geo Scan」を使っての測量作業は、現場でスマホやタブレットで動画撮影する要領で計測したい範囲をアプリに映して回るだけ。
ポイントごとにGNSS受信機を置くことで位置情報と計測データを重ね合わせて高精度の測量データを生成する。
3次元測量で計測したデータの活用も積極的に進められており、国土交通省では公共測量に3次元測量データを利用するためのマニュアルを策定。
また、標高を求めるガイドとして「ジオイド・モデル」を配布し、3次元測量データの実用化を進めている。
「OPTiM Geo Scan」もGNSS測量を行ったあと、ジオイド・モデルと組み合わせることで標高を付与した測量データを生成させることができる。
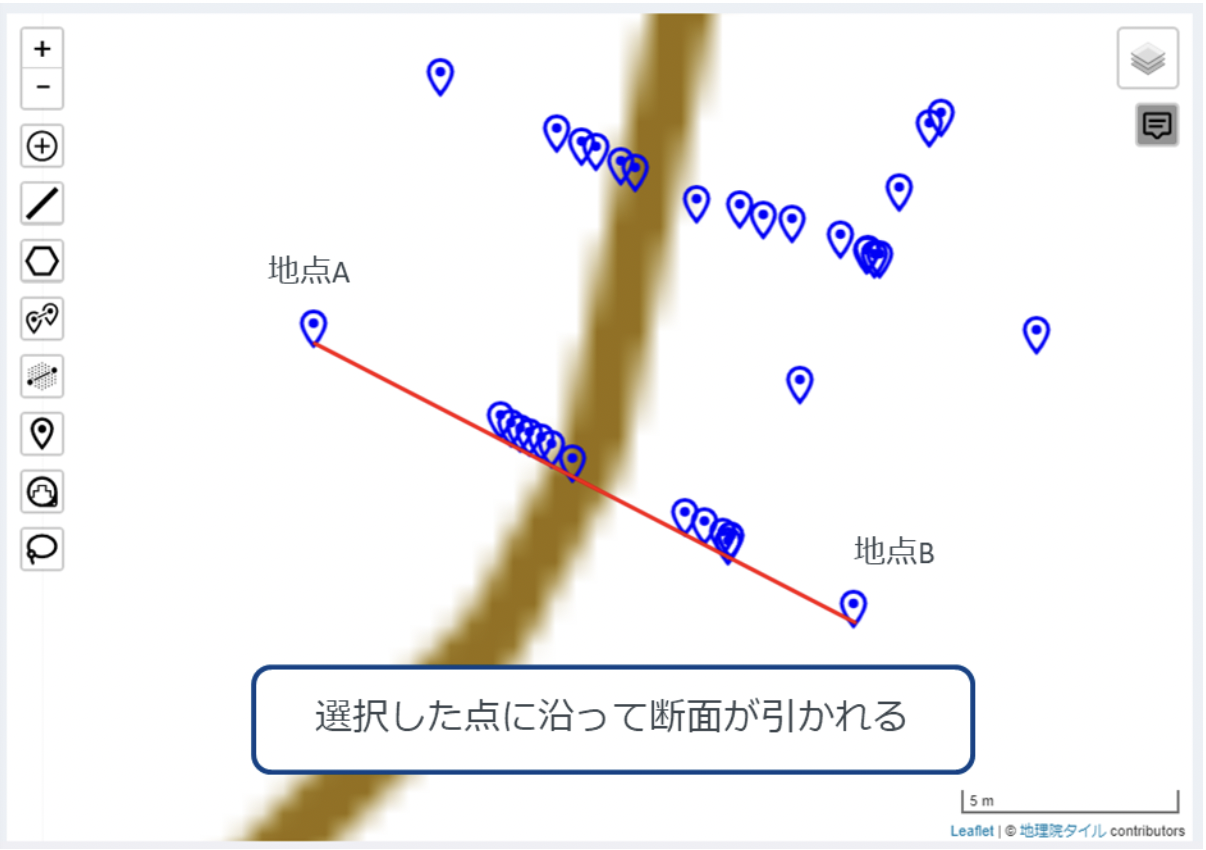
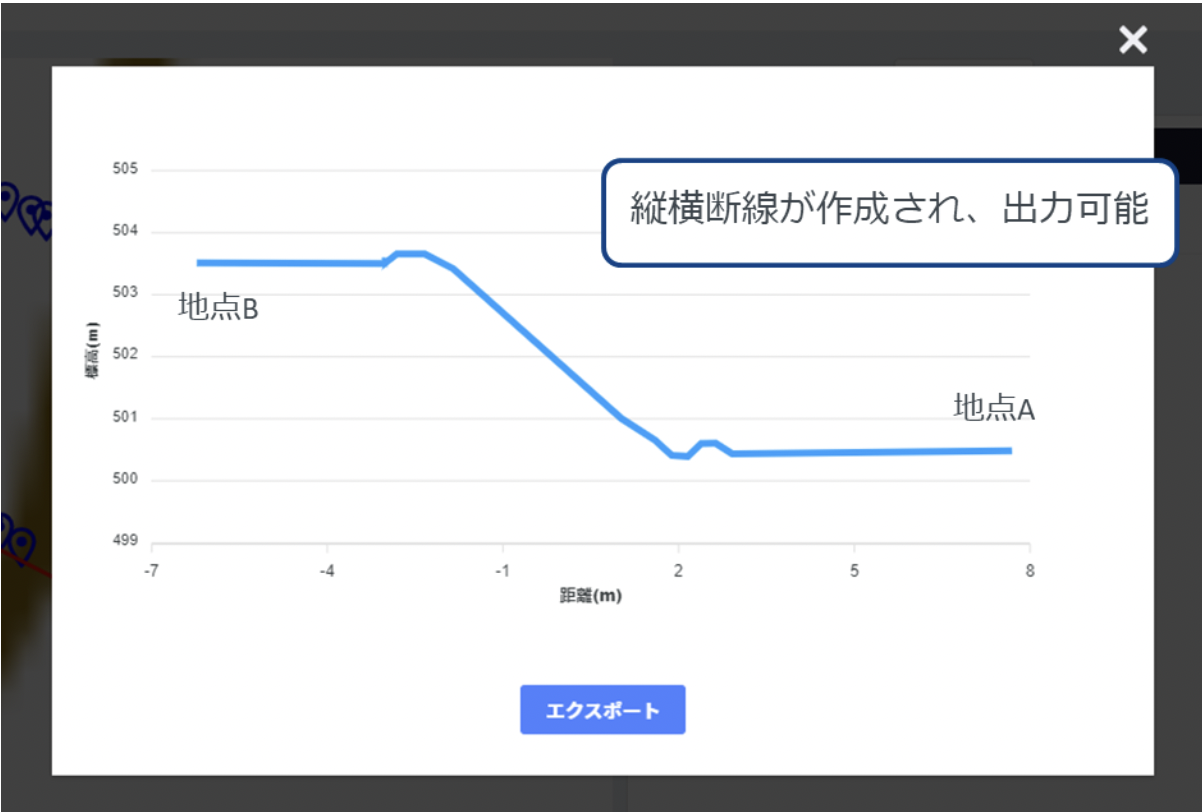
無料オプションの図化アプリ「OPTiM Geo Design」を使えば、縦横断面図・平面図の作成も可能だ。
3次元測量で取得した点群データは、処理ツールでひと手間加えることでさらに幅広い活用法がある。
Geo Scanはオンライン点群処理ソフト「スキャン・エックス」と連携させることで等高線図を作成したり、土量計算を行ったり、設計データと重ね合わせてシミュレーションを行うといった使い方もできる。
ICT化が進むと、トータルステーション(TS)の据え付け作業のような方法は必要なくなるかもしれない。
一方で、等高線図など図面の読み方や図面作成に用いる数値の求め方は共通しているので、もちろん知っておいて損はない。
実際に計算式を使って計算する機会は減るとしても、測量アプリや処理ソフトがどのような仕組みでデータを示しているかを知っておくことで、より高度な知識を理解できるようになる。
「OPTiM Geo Scan」のような最新の測量技術を実際に手に取り、測量手法の変化やデータの活用法に触れてみるのも大切なことだと言えるだろう。
まずは「等高線とは?」というところから、地形図の読み方など基礎をおさらいしよう。
測量士補試験に出題される、等高線の点間距離求め方も解説を行う。記事の後半では、等高線や標高に関する最新技術についても紹介していく。
等高線とは? 〜等高線からわかること〜
等高線(別名:コンターライン)とは、同じ高さの地点(標高)を結んだ線のことである。
間隔ごとに主曲線・計曲線・補助曲線の3種類の線があり、等高線からその場の地形を読み取ることができる。
主曲線・計曲線・補助曲線は線の太さや種類で見分けられるようになっている。
たとえば、5000分の1の地図では以下のような間隔で示される。
- 主曲線……実線(5mごと)。基本となる線で、原則として省略しない
- 計曲線……太い実線(25mごと)。主曲線5本ごとに計曲線が用いられる
- 補助曲線……破線(2.5mごと)地形を詳細に表現するべき箇所に使用。主曲線の1/2間隔
等高線の間隔が狭いと斜面は急で、広ければなだらかな地形である。
等高線から断面図を作成
等高線は上空から地面を見下ろすかたちで、地形を表現するものだが、地形を横から見た「断面図」を作成することもできる。
【断面図の作り方】
まず断面図を作成したい位置に直線を水平に引く。
次に、その直線と平行になるように100mごとの線を一定間隔で引く(高さを示す平行線のことを標高線という)。
直線と等高線が交わる点から、標高線に向けて垂線をおろし、高さごとの標高線と交わる点(下図の〇)を直線で結ぶと断面図が作成できる。
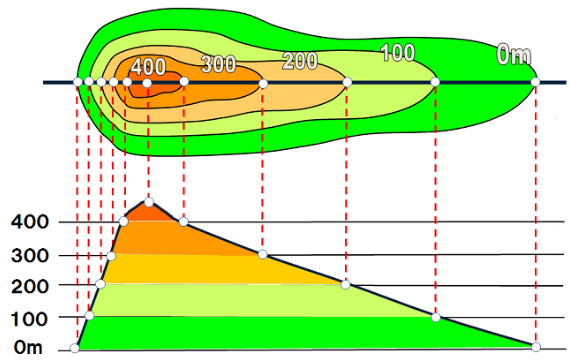
引用元:国土交通省 国土地理院「小学5年・6年のページ」(https://www.gsi.go.jp/KIDS/KIDS07.html)
まず断面図を作成したい位置に直線を水平に引く。
次に、その直線と平行になるように100mごとの線を一定間隔で引く(高さを示す平行線のことを標高線という)。
直線と等高線が交わる点から、標高線に向けて垂線をおろし、高さごとの標高線と交わる点(下図の〇)を直線で結ぶと断面図が作成できる。

引用元:国土交通省 国土地理院「小学5年・6年のページ」(https://www.gsi.go.jp/KIDS/KIDS07.html)
等高線図から尾根と谷を読み解く
等高線から地形が読み取れると前述したが、なんとなく地形の高低差の判別がつくだけではものたりない。
地形の最も高い部分の連なりを示す「尾根線」と、山と山の間の低地を結んだ「谷線」も覚えておこう。
- 尾根線:地形の最も高い部分の連なりを示す
- 谷線:山と山の間の低地を結んだ線
まずは等高線の中から最も標高の高い位置(山頂)と、川の位置を確認しよう。
水は高いところから低いところへ流れることもあり、川は地図上で低地を示している。そして、川の流れる場所が谷線の位置とも言える。
とはいえ、もちろん川が流れていない谷地もある。谷線の見つけ方は、もう一つ、高地から低地へ向かってみたとき、等高線がくぼんだ形状の場所が谷である。
 引用:国土交通省 国土地理院「地図を見て尾根と谷を読み解く」(https://www.gsi.go.jp/CHIRIKYOUIKU/one_tani.html)
引用:国土交通省 国土地理院「地図を見て尾根と谷を読み解く」(https://www.gsi.go.jp/CHIRIKYOUIKU/one_tani.html)一方で、高地から低地に向かって見たときに、突き出した形状の地形の突端が尾根線である(上記図の赤線が尾根線)。
尾根線は山頂と山頂をつなぐ線でもあるので、図面上のもっとも高い位置(山頂)をまず見ると良い。
等高線の点間距離の求め方
前項までに等高線に関する基礎知識を紹介してきた。
続いては、等高線に関する知識の活用法についてだ。
測量士補試験では、等高線の間隔(2点間の距離)を計算式で求める問題が出題されている。
よくある形式の例題を4つのステップに従い解いてみよう。
【問】
トータルステーションを用いた縮尺1/1000の地形図作成において。
標高125mの点Aから、ある道路上の点Bの観測を行ったところ、高低角-30°、斜距離86mの結果が得られた。
点Bから同じ道路上にある点Cを観測したところ、標高42mであった。このとき、点B,C間の水平距離を300mとすると、点Bと点Cを結ぶ道路とこれを横断する標高60mの等高線との交点xは、地形図上の点cから何㎝の地点か?
ただし、点Bと点Cを結ぶ道路は傾斜が一定でまっすぐな道路とする。
トータルステーションを用いた縮尺1/1000の地形図作成において。
標高125mの点Aから、ある道路上の点Bの観測を行ったところ、高低角-30°、斜距離86mの結果が得られた。
点Bから同じ道路上にある点Cを観測したところ、標高42mであった。このとき、点B,C間の水平距離を300mとすると、点Bと点Cを結ぶ道路とこれを横断する標高60mの等高線との交点xは、地形図上の点cから何㎝の地点か?
ただし、点Bと点Cを結ぶ道路は傾斜が一定でまっすぐな道路とする。

問題文を図で示すと上図になる。
問われているのは、交点xから垂直に降ろした点x´から点cまでの距離である。
一見難しく感じるかもしれないが、解法に慣れれば落ち着いて正解を出せるはずだ。
【解答Step.1】sin定義で高さを求める
まずは、高低角-30°とAB間の斜距離86mを使って、標高125mから点Bまでの高低差(h)を求める。
三角比のsinΘの定義を使うと高低差hの部分(=対辺)を求められる。

sinΘの定義
sinΘ = 対辺 / 斜辺 「斜辺」を両辺に掛けると・・・斜辺 × sinΘ = 対辺
この三角形は30°の角をもつ直角三角形なので、sin30°の関数※「1/2(0.5)」を利用する。
※測量士(補)試験では、関数表が問題文に添えられているが、sin30°は代表的なので暗記するとよい。
86m × sin30° = 86 × 0.5 = 43m
【解答Step.2】引き算で、点Bの標高と高低差(辺の長さ)を求める
ステップ1で標高125m地点と点Bまでの高低差を求めた。
続いては、点Bの標高を求める。

点Bを通る垂線を見れば、計算はシンプルだ。標高125mから43mを引けばよい。
125m ー 43m = 82m
点Bの標高は82mということがわかる。
次に、点Bから垂直に降ろされた線の長さを求める。こちらも引き算を使うだけだ。
点Bの標高82mから点cに示されている標高42mを引く。
82m ー 42m = 40m
大きい三角形の高低差は40mということがわかる。
【解答Step.3】比例式を使って、辺の長さを求める
ここから後半戦で、交点 x に関係する計算に突入する。
まずは、交点xから標高42mまでの高低差を出そう。
交点xは標高60mとわかっているので、引き算で求められる。

続いては三角比の比例式を使う。
点cと点bを斜辺に持つ大きな三角形と、点cと交点xを斜辺に持つ小さな三角形は角cが等しい相似の三角形である。
この2つの三角形の辺の長さを比例式にすることで、点x´から点cまでの長さ、つまり交点xと点cの水平距離を求める。
大きな三角形の高さ:底辺の長さ = 小さな三角形の高さ:底辺の長さ
40 : 300 = 18 : y
両辺の外側の数字同士、内側の数字同士を掛ける
40 × y = 300 × 18
40y = 5400
y = 135
40y = 5400
y = 135
交点xと点cの水平距離は135m
【解答step.4】縮尺を合わせる
最後に、地形図の縮尺を条件に合わせて完成だ。
問題文に縮尺1/1000と書いてあるので、1000で割り、単位を㎝に揃える。
135m ÷ 1000 = 0.135m
0.135m = 13.5㎝
答え、13.5㎝
0.135m = 13.5㎝
答え、13.5㎝
トータルステーション(TS)の据え付けや高低差計算は必要なし!最新の測量技術を紹介!
トータルステーション(TS)で慎重に観測し、標高や高低差を計算式で求めるというやり方は、伝統的な測量技術の一つ。
いまも測量士(補)国家資格を取るために習得すべき知識とされている。
しかし、実務においては、最新技術によって測量作業は効率化し、図面作成も素早くできるようになってきている。
3次元測量は、地上型レーザースキャナーやGNSS(人工衛星)を用いて3次元座標を取得し、それを活用して測量データを生成する。
複雑な地形に強く、1人で作業を完了させられるものも。また、取得したデータを様々な形で活用できるというメリットもある。
2022年には国土交通省が「3次元測量技術を用いた出来形管理要領(案)」の改訂版を策定し、“これからの測量技術”として注目が高まっている。

「OPTiM Geo Scan」は、iPhone pro/iPad proシリーズに搭載されているLiDARというレーザー計測技術を利用した3次元測量アプリで、スマホやタブレットとハンディサイズのGNSS受信器を使って1人で測量が行える。
手軽でありながら、出来形管理要領に準拠しており実用性は十分だ。

「OPTiM Geo Scan」を使っての測量作業は、現場でスマホやタブレットで動画撮影する要領で計測したい範囲をアプリに映して回るだけ。
ポイントごとにGNSS受信機を置くことで位置情報と計測データを重ね合わせて高精度の測量データを生成する。
標高表示や等高線生成がラクラク!スマホ測量アプリ「OPTiM Geo Scan」
3次元測量で計測したデータの活用も積極的に進められており、国土交通省では公共測量に3次元測量データを利用するためのマニュアルを策定。
また、標高を求めるガイドとして「ジオイド・モデル」を配布し、3次元測量データの実用化を進めている。
「OPTiM Geo Scan」もGNSS測量を行ったあと、ジオイド・モデルと組み合わせることで標高を付与した測量データを生成させることができる。

無料オプションの図化アプリ「OPTiM Geo Design」を使えば、縦横断面図・平面図の作成も可能だ。
3次元測量で取得した点群データは、処理ツールでひと手間加えることでさらに幅広い活用法がある。

Geo Scanはオンライン点群処理ソフト「スキャン・エックス」と連携させることで等高線図を作成したり、土量計算を行ったり、設計データと重ね合わせてシミュレーションを行うといった使い方もできる。
ICT化が進むと、トータルステーション(TS)の据え付け作業のような方法は必要なくなるかもしれない。
一方で、等高線図など図面の読み方や図面作成に用いる数値の求め方は共通しているので、もちろん知っておいて損はない。
実際に計算式を使って計算する機会は減るとしても、測量アプリや処理ソフトがどのような仕組みでデータを示しているかを知っておくことで、より高度な知識を理解できるようになる。
「OPTiM Geo Scan」のような最新の測量技術を実際に手に取り、測量手法の変化やデータの活用法に触れてみるのも大切なことだと言えるだろう。
参考:
https://digital-construction.jp/column/1295
https://digital-construction.jp/column/1325
https://www.gsi.go.jp/KIDS/KIDS07.html https://fgd.gsi.go.jp/download/geoid.php https://www.gsi.go.jp/gijyutukanri/gijyutukanri41021.html chrome-extension://efaidnbmnnnibpcajpcglclefindmkaj/https://ocf.or.jp/img/seminar2016/02_serizawa_n.pdf
https://digital-construction.jp/column/1295
https://digital-construction.jp/column/1325
https://www.gsi.go.jp/KIDS/KIDS07.html https://fgd.gsi.go.jp/download/geoid.php https://www.gsi.go.jp/gijyutukanri/gijyutukanri41021.html chrome-extension://efaidnbmnnnibpcajpcglclefindmkaj/https://ocf.or.jp/img/seminar2016/02_serizawa_n.pdf
WRITTEN by

三浦 るり
2006年よりライターのキャリアをスタートし、2012年よりフリーに。人材業界でさまざまな業界・分野に触れてきた経験を活かし、幅広くライティングを手掛ける。現在は特に建築や不動産、さらにはDX分野を探究中。
大人気シリーズ!【いまさら聞けない?】測量のことイチから解説 〜 連載記事一覧 〜
- 等高線の基礎知識を押さえよう!〜点間距離の求め方など応用知識も紹介!〜【測量のことイチから解説】
