コラム・特集
【三角関数】をおさらい! 〜 測量士(補)試験に頻出!忘れた!という方、必見!〜【測量のことイチから解説】」


近年、人工衛星やドローンを利用する3次元測量も増えてきているが、かつては「三角関数」を用いた“三角測量”がスタンダードであった。
そういったこともあり、測量士(測量士補)試験では、三角関数を用いる計算問題もいまだ出題される。そこで今回は、測量に関する「三角関数」についておさらいしよう。
三角関数と測量は共に歴史を築いてきたと言っても過言ではない。
古代エジプトの数学者タレスは影の長さを利用してピラミッドの高さを求めた。
45度の三角定規は直角を挟む2つの辺の長さが等しいことは覚えているだろうか。
陽の差す角度が45度のときに身長と影の長さが等しくなることに気付いたタレスは、影の長さからピラミッドの高さを推測したのだ。
そして、タレスの手法を応用し、“三角形の比”と1辺の長さを用いて直接測ることのできない点までの距離を計算する方式が見いだされた。それが「三角測量」である。
その後、三角測量は古代エジプトから1980年代までの2000年以上も使われ続けた。
初期の三角測量では直角三角形の比が用いられていたが、17世紀のヨーロッパで角度が90度以上の三角形からも測定したい点までの距離を算出するやり方が発見された。これが三角関数の起源である。
近代の三角測量は、「三角形の一辺とその両端角がわかれば三角形が確定する」という性質を利用して、直接測ることのできない点を測定していた。
なお、基準となる“三角形の一辺”のことを「基線」と呼ぶ。
三角関数は測量の歴史の中で生れ、発展してきたと。
とはいえ、三角関数は測量のためだけのものではなく、数学はもちろん、物理の世界などでも応用され、さまざまな場面で活用されるようになった。
現代においては、土木・建設業のほかに製造業の設計工程で頻繁に使われている。また、ゲームでは、キャラクターがジャンプする動き、影の長さなどCG(コンピュータ・グラフィック)処理において欠かせないものとなっている。
この他、三角関数は「波形」を表現できることから、電波や音波、光波などを制御するのにも使われる。
家電でいえば、外側の筐体デザインから機能面までいくつもの箇所で三角関数が使われているのだ。
測量士(測量士補)国家試験では三角関数を用いる計算問題が出題される。
三角関数は、現在は主に高校数学の2年次に学習する単元であるが、過去には義務教育期間の中学校で指導されていたこもある。
その一方で、高校でも文系コースなどでは学習しないケースもある。
本項では、三角形の基礎知識として、三角定規の形のもととなっているピタゴラスの定理(三平方の定理)と、その発展形である三角関数をおさらいしよう。
「ピタゴラスの定理(三平方の定理)」とは、「直角三角形において、斜辺の2乗の和は、他の2辺の2乗の和に等しい」というもの。
三角関数は、Θ(シータ)という角度を表す記号を用いた式になる。
そして、三角形の辺の比には、それぞれサイン(sin/正弦)、コサイン(cos/余弦)、タンジェント(tan/正接)という名称が付いている。
下図の直角三角形でサイン、コサイン、タンジェントの位置を見てみよう。
三角関数の計算に取り組むために、三角形の比(サイン・コサイン・タンジェント)の定義をまずは覚えよう。
Θと2つの辺の位置関係をしっかりと押さえることがポイントとなる。
そもそも三角関数は90度以上の角を含む三角形で用いられるのだが、測量士(測量士補)試験では直角三角形を使った問題が基本となっている。
問題文にある関数表を活用して定義に数字を当てはめ解を求めるという流れだ。
変わった形の三角形が出題されることは恐れず、まずは過去問題にあたり計算の仕方に慣れるといいだろう。
三角関数が基になっている三角測量は、日本では明治から長きにわたり使用されてきた。
その後、平成に入りGPSの運用が本格的にはじまり、GPSを使った測量手法も開発された。GPSのほかに人工衛星の種類も増えてき、これらはまとめてGNSS(全球測位衛星システム)測量と呼ばれるようになった。
GNSS測量では、複数の人工衛星から送信された信号を、地上の受信機で受信することにより、電波が届くまでにかかった時間から位置情報に変換する。三角測量とは測位を行う仕組みが根本から異なるのだ。
三角測量とGNSS測量とでは、測位方法だけではなく、作業手順や作業ツールも大きくことなる。
土木・建設業界ではなじみ深いTS(トータルステーション)に機能追加されているようなものもあるが、スマホなど、最新機器を使うようなものもある。
「OPTiM Geo Scan」はスマートフォンやタブレットとGNSSレシーバーだけで、1人で測量作業を行えるスマホ測量アプリだ。
測量士の国家資格合格には300時間以上必要と一般的に言われているが、「OPTiM Geo Scan」は30分程度で一通りの操作を把握できるほど扱いやすく、それでいて高精度の測量を実現。
アプリで取得した3次元データは国土交通省出来形管理要領に準拠した精度で、実用性も申し分ない。操作方法は、まず、アプリ※の画面を開き、ビデオ撮影をするように測量したい範囲を映す。


続いてハンディサイズのGNSSレシーバーをポイントごとに設置して画面をタップする。こうすることで、アプリ内でGNSSレシーバーが取得した位置情報と3次元測量データが紐づけられ高精度の測量データが生成される。
取得データはその場で確認できるだけでなく、クラウド上にアップすることでほぼリアルタイムで遠隔でも確認が可能だ。
※「OPTiM Geo Scan」はiPhone 12 pro以降の機種/iPad proシリーズに対応。
また、3次元測量だけでなく、座標データを取得したい場合、GNSS測量と杭打ちができる「OPTiM Geo Point」を無料オプションで利用できる。杭打ち作業が一人でこなせる便利なツールだ。


さらに後工程用に図化アプリ「OPTiM Geo Desgin」が同じく無料オプションとして利用可能。これを使えば、平面図、縦断図、横断図など2次元図面に必要な図形データが作成できる。
かつては測量業務に携わるために三角関数など基礎知識の取得にも時間を取られていた。それが今ではスマホゲームを操作するような感覚で、簡単に測量が行えてしまうのだ。
あらゆる場面でデジタル化が進んでいる現代、測量から書類作成までスムーズな製品を選ぶことで業務は大幅に効率化させられる。
そういったこともあり、測量士(測量士補)試験では、三角関数を用いる計算問題もいまだ出題される。そこで今回は、測量に関する「三角関数」についておさらいしよう。
三角関数は測量から生まれた!?
三角関数と測量は共に歴史を築いてきたと言っても過言ではない。
古代エジプトの数学者タレスは影の長さを利用してピラミッドの高さを求めた。
45度の三角定規は直角を挟む2つの辺の長さが等しいことは覚えているだろうか。
陽の差す角度が45度のときに身長と影の長さが等しくなることに気付いたタレスは、影の長さからピラミッドの高さを推測したのだ。
そして、タレスの手法を応用し、“三角形の比”と1辺の長さを用いて直接測ることのできない点までの距離を計算する方式が見いだされた。それが「三角測量」である。
その後、三角測量は古代エジプトから1980年代までの2000年以上も使われ続けた。
初期の三角測量では直角三角形の比が用いられていたが、17世紀のヨーロッパで角度が90度以上の三角形からも測定したい点までの距離を算出するやり方が発見された。これが三角関数の起源である。
近代の三角測量は、「三角形の一辺とその両端角がわかれば三角形が確定する」という性質を利用して、直接測ることのできない点を測定していた。
なお、基準となる“三角形の一辺”のことを「基線」と呼ぶ。
こんなところにも使われている「三角関数」
三角関数は測量の歴史の中で生れ、発展してきたと。
とはいえ、三角関数は測量のためだけのものではなく、数学はもちろん、物理の世界などでも応用され、さまざまな場面で活用されるようになった。
現代においては、土木・建設業のほかに製造業の設計工程で頻繁に使われている。また、ゲームでは、キャラクターがジャンプする動き、影の長さなどCG(コンピュータ・グラフィック)処理において欠かせないものとなっている。
この他、三角関数は「波形」を表現できることから、電波や音波、光波などを制御するのにも使われる。
家電でいえば、外側の筐体デザインから機能面までいくつもの箇所で三角関数が使われているのだ。
三角関数をおさらい
測量士(測量士補)国家試験では三角関数を用いる計算問題が出題される。
三角関数は、現在は主に高校数学の2年次に学習する単元であるが、過去には義務教育期間の中学校で指導されていたこもある。
その一方で、高校でも文系コースなどでは学習しないケースもある。
本項では、三角形の基礎知識として、三角定規の形のもととなっているピタゴラスの定理(三平方の定理)と、その発展形である三角関数をおさらいしよう。
ピタゴラスの定理(三平方の定理)
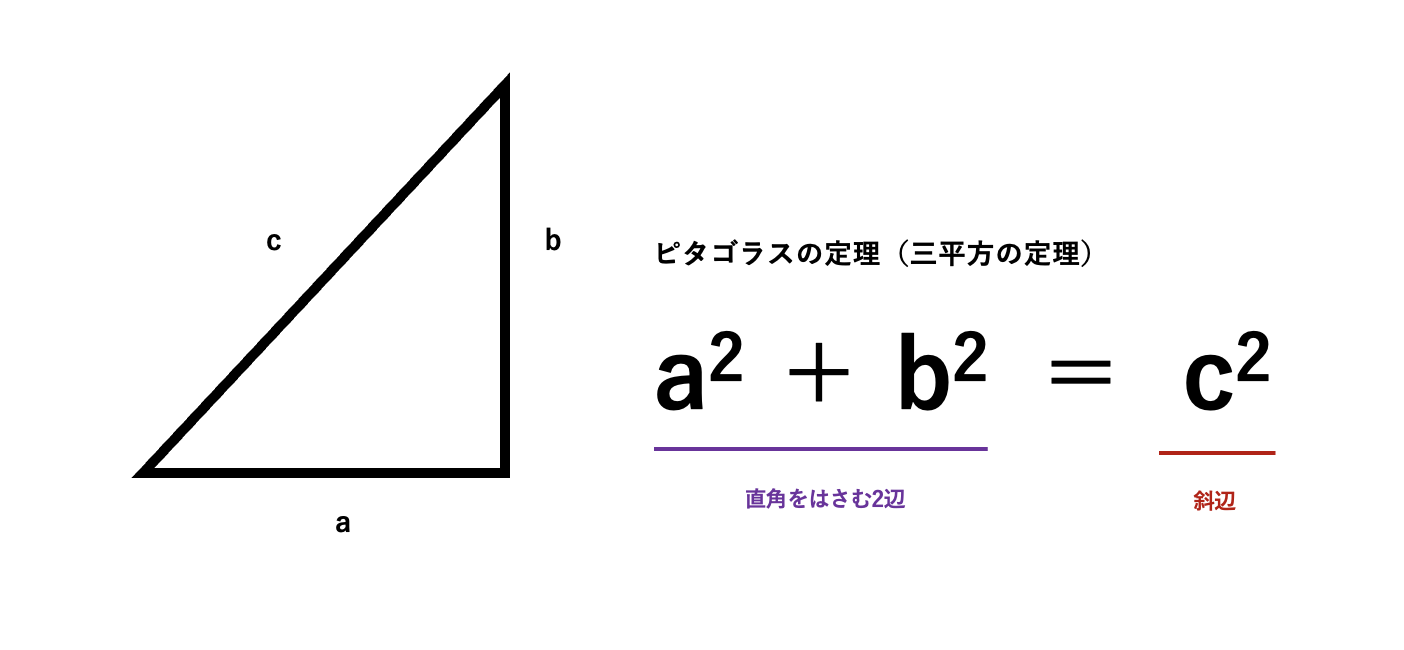
「ピタゴラスの定理(三平方の定理)」とは、「直角三角形において、斜辺の2乗の和は、他の2辺の2乗の和に等しい」というもの。

直角三角形の3辺の長さをa、b、c(長辺)とした時
「a2+b2=c2」という算式となる。
「a2+b2=c2」という算式となる。
サインΘ、コサインΘ、タンジェントΘの定義
三角関数は、Θ(シータ)という角度を表す記号を用いた式になる。
そして、三角形の辺の比には、それぞれサイン(sin/正弦)、コサイン(cos/余弦)、タンジェント(tan/正接)という名称が付いている。
下図の直角三角形でサイン、コサイン、タンジェントの位置を見てみよう。
- 斜辺と高さの比→サイン(sin/正弦)
- 斜辺と底辺の比→コサイン(cos/余弦)
- 底辺と高さの比→タンジェント(tan/正接)
三角関数の計算に取り組むために、三角形の比(サイン・コサイン・タンジェント)の定義をまずは覚えよう。
Θと2つの辺の位置関係をしっかりと押さえることがポイントとなる。
- sinΘ=b/a
- cosΘ=c/a
- tanΘ=b/c
そもそも三角関数は90度以上の角を含む三角形で用いられるのだが、測量士(測量士補)試験では直角三角形を使った問題が基本となっている。
問題文にある関数表を活用して定義に数字を当てはめ解を求めるという流れだ。
変わった形の三角形が出題されることは恐れず、まずは過去問題にあたり計算の仕方に慣れるといいだろう。
三角測量とGNSS測量
三角関数が基になっている三角測量は、日本では明治から長きにわたり使用されてきた。
その後、平成に入りGPSの運用が本格的にはじまり、GPSを使った測量手法も開発された。GPSのほかに人工衛星の種類も増えてき、これらはまとめてGNSS(全球測位衛星システム)測量と呼ばれるようになった。
GNSS測量では、複数の人工衛星から送信された信号を、地上の受信機で受信することにより、電波が届くまでにかかった時間から位置情報に変換する。三角測量とは測位を行う仕組みが根本から異なるのだ。
三角関数の知識がなくても高精度測量ができるスマホ測量アプリ「OPTiM Geo Scan」
三角測量とGNSS測量とでは、測位方法だけではなく、作業手順や作業ツールも大きくことなる。
土木・建設業界ではなじみ深いTS(トータルステーション)に機能追加されているようなものもあるが、スマホなど、最新機器を使うようなものもある。
「OPTiM Geo Scan」はスマートフォンやタブレットとGNSSレシーバーだけで、1人で測量作業を行えるスマホ測量アプリだ。
測量士の国家資格合格には300時間以上必要と一般的に言われているが、「OPTiM Geo Scan」は30分程度で一通りの操作を把握できるほど扱いやすく、それでいて高精度の測量を実現。
アプリで取得した3次元データは国土交通省出来形管理要領に準拠した精度で、実用性も申し分ない。操作方法は、まず、アプリ※の画面を開き、ビデオ撮影をするように測量したい範囲を映す。


続いてハンディサイズのGNSSレシーバーをポイントごとに設置して画面をタップする。こうすることで、アプリ内でGNSSレシーバーが取得した位置情報と3次元測量データが紐づけられ高精度の測量データが生成される。
取得データはその場で確認できるだけでなく、クラウド上にアップすることでほぼリアルタイムで遠隔でも確認が可能だ。
※「OPTiM Geo Scan」はiPhone 12 pro以降の機種/iPad proシリーズに対応。
3次元測量アプリ「OPTiM Geo Scan」は測位以外の機能も充実!
また、3次元測量だけでなく、座標データを取得したい場合、GNSS測量と杭打ちができる「OPTiM Geo Point」を無料オプションで利用できる。杭打ち作業が一人でこなせる便利なツールだ。


さらに後工程用に図化アプリ「OPTiM Geo Desgin」が同じく無料オプションとして利用可能。これを使えば、平面図、縦断図、横断図など2次元図面に必要な図形データが作成できる。
かつては測量業務に携わるために三角関数など基礎知識の取得にも時間を取られていた。それが今ではスマホゲームを操作するような感覚で、簡単に測量が行えてしまうのだ。
あらゆる場面でデジタル化が進んでいる現代、測量から書類作成までスムーズな製品を選ぶことで業務は大幅に効率化させられる。
参考:
https://www.dainippon-tosho.co.jp/newsletter/files/pyramid.pdfhttps://club.informatix.co.jp/?p=5074
https://diamond.jp/articles/-/213650https://kou.benesse.co.jp/nigate/math/a14m0313.html
https://www.gsi.go.jp/common/000220103.pdf
https://www.agaroot.jp/sokuryoshi/column/study-hours/
https://www.dainippon-tosho.co.jp/newsletter/files/pyramid.pdfhttps://club.informatix.co.jp/?p=5074
https://diamond.jp/articles/-/213650https://kou.benesse.co.jp/nigate/math/a14m0313.html
https://www.gsi.go.jp/common/000220103.pdf
https://www.agaroot.jp/sokuryoshi/column/study-hours/
WRITTEN by

三浦 るり
2006年よりライターのキャリアをスタートし、2012年よりフリーに。人材業界でさまざまな業界・分野に触れてきた経験を活かし、幅広くライティングを手掛ける。現在は特に建築や不動産、さらにはDX分野を探究中。
大人気シリーズ!【いまさら聞けない?】測量のことイチから解説 〜 連載記事一覧 〜
- 【三角関数】をおさらい! 〜 測量士(補)試験に頻出!忘れた!という方、必見!〜【測量のことイチから解説】」
